BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
ỨNG DỤNG NHỮNG TÍNH NĂNG MỚI VỀ PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH CỦA CASIO FX- 580VNX VÀO GIẢI TOÁN
- 21/02/2019
- 761 lượt xem
Bên cạnh các tính năng đã có trong máy tính Casio fx – 570Vn Plus như giải phương trình bậc 2 và bậc 3; hệ phương trình 2 ẩn và 3 ẩn, Casio fx 580 vnx còn bổ sung thêm các tính năng hữu ích như:
- Giải phương trình bậc 4
- Giải hệ 4 phương trình 4 ẩn số
- Lưu lại các nghiệm vào các ô nhớ
- Cực trị hàm số bậc 3
- Thông báo vô nghiệm và vô số nghiệm
- Nhập trực tiếp các phép tính đạo hàm, tích phân,… vào các hệ số
- Đặc biệt, Casio fx 580 vnx bổ sung thêm phương thức giải bất phương trình
Dưới đây là một số bài toán minh họa việc ứng dụng các tính năng mới trong phương thức giải phương trình, hệ phương trinh và bất phương trình:
Bài toán 1. Trong không gian $latex Oxyz$ cho các điểm $latex A\left( 9;12;15 \right)$ và mặt phẳng $latex \left( P \right):4x+5y+6z-32=0$ . Tìm tọa độ $latex {A}’$ là hình chiếu vuông góc của điểm $latex A$ trên mặt phẳng $latex \left( P \right)$
- $latex {A}’\left( 1;2;3 \right)$
- $latex {A}’\left( -4;6;3 \right)$
- $latex {A}’\left( 2;0;4 \right)$
- $latex {A}’\left( 1;-2;-1 \right)$
Hướng dẫn giải.
VTPT của mặt phẳng $latex \left( P \right)$ là $latex \vec{n}=\left( 4;5;6 \right)$
Gọi $latex d$ là đường thẳng đi qua A và vuông góc với $latex \left( P \right)$. Khi đó phương trình đường thẳng $latex d$ có dạng $latex \left\{ \begin{align} & x=9+4t \\ & y=12+5t \\ & z=15+6t \\\end{align} \right.$
Vì $latex {A}’$ là hình chiếu vuông góc của điểm $latex A$ trên mặt phẳng $latex \left( P \right)$ nên ta có $latex {A}’\in d$ và $latex {A}’\in \left( P \right)$
Sử dụng w9 trong Casio fx– 580 vnx giải hệ phương trình để tìm tọa độ điểm $latex {A}’$ là $latex \left\{ \begin{align} & x+4t=9 \\& y+5t=12 \\& z+6t=15 \\& 4x+5y+6z=32 \\\end{align} \right.$
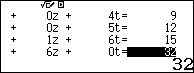
Chọn đáp án A
Bài toán 2. Phương trình mặt cầu đi qua các điểm $latex A\left( -2;1;4 \right)$; $latex B\left( 1;2;-3 \right)$; $latex C\left( 2;1;3 \right)$ và $latex D\left( -2;1;7 \right)$ là:
- $latex {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-6y-11z+88=0$
- $latex {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x-64y-12z+88=0$
- $latex {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-x-67y-11z+88=0$
- $latex {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-60y-10z+80=0$
Hướng dẫn giải
Phương trình mặt cầu có dạng: $latex {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2ax-2by-2cz+d=0$
Do $latex A,B,C$ và $latex D$ thuộc mặt cầu nên ta có hệ phương trình: $latex \left\{ \begin{align}& 4x-2y-8z+t=-21 \\& -2x-4y+6z+t=-14 \\ & -4x-2y-6z+t=-14 \\ & 4x-2y-14z+t=-54 \\\end{align} \right.$
Sử dụng w9 trong Casio fx 580 vnx giải hệ phương trình
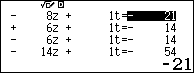
Nghiệm thu được là:
Vậy phương trình mặt cầu cần tìm là: $latex {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-x-67y-11z+88=0$
Chọn câu C
Bài toán 3. Tìm nghiệm của phương trình sau: $latex \sqrt{5{{x}^{2}}+14x+9}-\sqrt{{{x}^{2}}-x-20}=5\sqrt{x+1}$
Hướng dẫn giải
Tìm tập xác định: Sử dụng tính năng giải bất phương trình của Casio fx 580 vnx để tìm tập xác định của phương trình
Điều kiện bài toán có nghĩa $latex \left\{ \begin{align} & 5{{x}^{2}}+14x+9\ge 0 \\ & {{x}^{2}}-x-20\ge 0 \\ & x+1\ge 0 \\ \end{align} \right.$
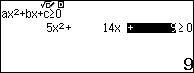
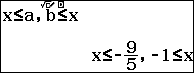
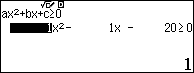
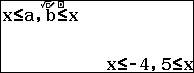
Suy ra tập xác định: $latex x\ge 5$
Khai triển và giải phương trình
$\sqrt{5{{x}^{2}}+14x+9}-\sqrt{{{x}^{2}}-x-20}=5\sqrt{x+1}\\$
$\Leftrightarrow \sqrt{5{{x}^{2}}+14x+9}=\sqrt{{{x}^{2}}-x-20}+5\sqrt{x+1}\\$
$\Leftrightarrow 5{{x}^{2}}+14x+9={{x}^{2}}+24x-5+10\sqrt{\left( {{x}^{2}}-x-20 \right)\left( x+1 \right)}\\$
$\Leftrightarrow 4{{x}^{2}}-10x+4=10\sqrt{{{x}^{3}}-21x-20}\\$
$\Leftrightarrow 4{{x}^{4}}-20{{x}^{3}}+33{{x}^{2}}-20x+4=25\left( {{x}^{3}}-21x-20 \right)\\$
$\Leftrightarrow 4{{x}^{4}}-45{{x}^{3}}+33{{x}^{2}}+505x+504=0\\$
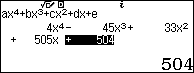
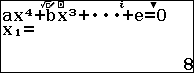
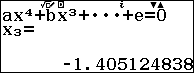
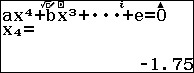
Do hai nghiệm $latex {{x}_{2}}$ và $latex {{x}_{3}}$ biểu hiện ở dạng số thập phân do đó ta có thể lưu hai nghiệm đó vào ô nhớ A và B và áp dụng định lý Viet vào phương trình bậc 2.
Suy ra $latex {{x}_{2}}$ và $latex {{x}_{3}}$ là nghiệm của phương trình bậc 2 $latex {{x}^{2}}-5x-9=0$
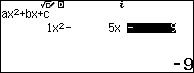
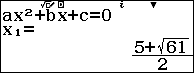
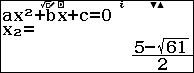
Kiểm tra lại điều kiện của TXĐ ta có $latex x=8$ và $latex x=\dfrac{5+\sqrt{61}}{2}$ là nghiệm của phương trình đã cho
Để hiểu rõ hơn cách sử dụng các tính năng mới của máy tính Casio fx 580 vnx của phương thức phương trình, hệ phương trình và bất phương trình bạn đọc có thể tham khảo thêm các video từ kênh Youtube của Diễn đàn máy tính cầm tay
Cảm ơn các bạn đã theo dõi bài viết ỨNG DỤNG NHỮNG TÍNH NĂNG MỚI VỀ PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH CỦA CASIO FX- 580VNX VÀO GIẢI TOÁN. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
