BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
ỨNG DỤNG MÁY TÍNH FX-880BTG GIẢI CÁC BÀI TOÁN LOGARIT TRONG ĐỀ THI THPT CÁC NĂM GẦN ĐÂY
- 06/10/2022
- 1,537 lượt xem
Câu 1: (Đề thi THPT năm 2021 mã đề 114) Với mọi $a, b$ thoả mãn $\log_{2}{a^3}+\log_{2}{b}=5$, khẳng định nào sau đây là đúng?
A. $a^3b=32$ B. $a^3b=25$ C. $a^3+b=32$ D. $a^3+b=25$
Lời giải
Chọn 1 giá trị a bất kì.
Lưu giá giá trị đó vào biến nhớ A.
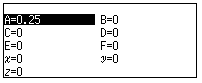
Dùng tính năng bộ giải phương trình
Nhập $\log_{2}{A^3}+\log_{2}{B}=5$. Tính giá trị của B
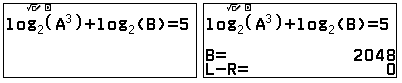
Nhập $A^3B-32$, $A^3B-25$, $A^3+B-32$, $A^3+B-25$. Kết quả bằng $0$ là đáp án đúng.
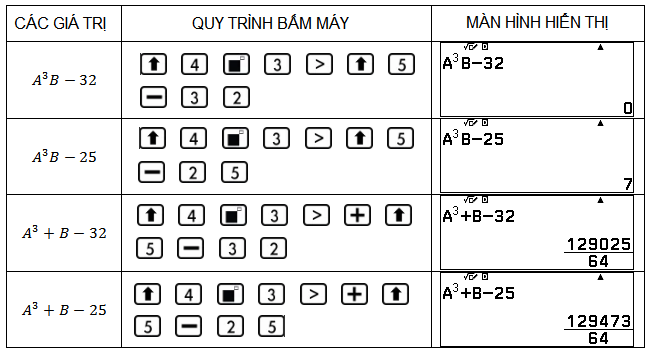
Chọn A.
Câu 2: (Đề thi THPT năm 2022 mã đề 112) Với $a, b$ là các số thực dương tuỳ ý và $a≠1$, $log_\dfrac{1}{a}\dfrac{1}{b^3}$
A. $3log_{a}b$ B. $log_{a}b$ C. $-3log_{a}b$ D. $\dfrac{1}{3}log_{a}b$
Lời giải
Chọn 1 giá trị a bất kì. Lưu giá trị đó vào biến nhớ A
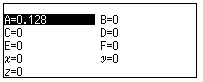
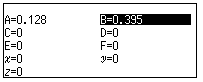
Chọn 1 giá trị b bất kì. Lưu giá trị đó vào biến nhớ B
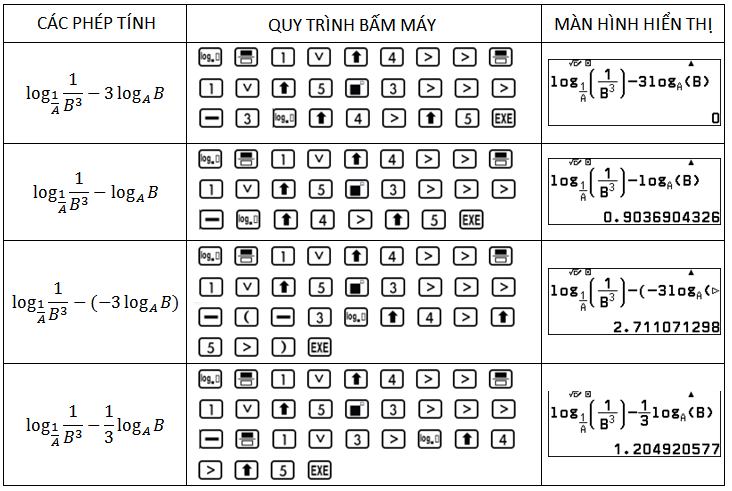
Nhập $log_\dfrac{1}{A}\dfrac{1}{B^3}-3log_{A}B$, $log_\dfrac{1}{A}\dfrac{1}{B^3}-log_{A}B$, $log_\dfrac{1}{A}\dfrac{1}{B^3}-(-3log_{A}B)$, $log_\dfrac{1}{A}\dfrac{1}{B^3}-\dfrac{1}{3}log_{A}B$. Kết quả bằng $0$ là đáp án đúng.
Chọn A.
About Toanbitexdtgd1
