BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG MÁY TÍNH FX-880BTG GIẢI BÀI TOÁN CỰC TRỊ SỐ PHỨC
- 31/03/2023
- 409 lượt xem
Đề bài: Cho số phức $z$ thỏa mãn $\begin{vmatrix}(1+i)z+1-7i\end{vmatrix}=\sqrt{2}$. Gọi $M,m$ lần lượt là giá trị lớn nhất và nhỏ nhất của $\begin{vmatrix}z\end{vmatrix}$. Tính giá trị của $M^{2}-m^{2}$
A. 34 B. 52 C.46 D. 50
Lời giải
Ta có $\begin{vmatrix}(1+i)z+1-7i\end{vmatrix}=\sqrt{2}$
$\Leftrightarrow \begin{vmatrix}
(1+i).\begin{pmatrix}
z+\dfrac{1-7i}{1+i}
\end{pmatrix}
\end{vmatrix}=\sqrt{2}$
$\Leftrightarrow \begin{vmatrix}
(1+i)
\end{vmatrix}.\begin{vmatrix}
z+\dfrac{1-7i}{1+i}
\end{vmatrix}=\sqrt{2}$
Sử dụng tính năng số phức trên máy tính Fx-880BTG
Mở tính năng số phức
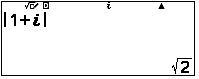
Tính $\begin{vmatrix}1+i\end{vmatrix}$
Tính $\dfrac{1-7i}{1+i}$
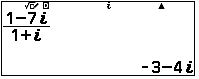
Phương trình $\Leftrightarrow \sqrt{2}.\begin{vmatrix}z-3-4i\end{vmatrix}=\sqrt{2}$
$\Leftrightarrow \begin{vmatrix}z-3-4i\end{vmatrix}=1$
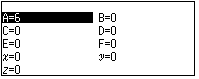
Tính Max$\begin{vmatrix}z\end{vmatrix}=\begin{vmatrix}-3-4i\end{vmatrix}+1$
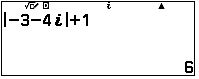
Lưu vào $A$
Tính Min$\begin{vmatrix}z\end{vmatrix}=\begin{vmatrix}-3-4i\end{vmatrix}-1$
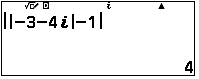
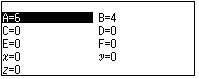
Lưu vào $B$
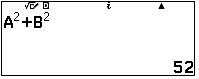
Tính giá trị $M^{2}-m^{2}$
Chọn B
Chia sẻ
About Toanbitexdtgd1
