BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG BẢNG TÍNH CỦA MÁY TÍNH KHOA HỌC FX-880BTG ĐỂ GIẢI BÀI TOÁN HÀM MŨ
- 29/11/2022
- 828 lượt xem
Bài 1: Số nghiệm của phương trình $6.4^x-2.6^{x+1}+6.9^x=0$ là
A. 3 B. 1 C. 2 D. 0
Lời giải
Cách 1: Sử dụng tính năng bảng giá trị của máy tính Casio Fx-880BTG.
Khới động chức năng bảng giá trị.
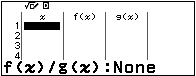
Chuyển bảng tính về tính 1 hàm $f(x)$.
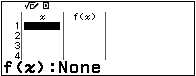
Nhập hàm số $f(x)=6.4^x-2.6^{x+1}+6.9^x$.
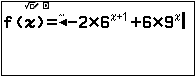
Thiết lập miền giá trị Start: $-10$ End: $10$ Step: $1$.
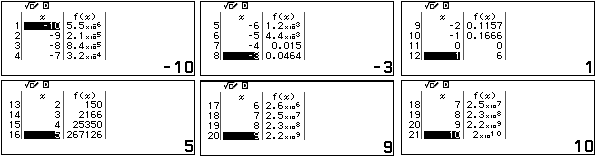
Ta thấy khi $x=0$ thì $f(x)=0$ vậy $x=0$ là nghiệm của phương trình.
Tiếp tục quan sát giá trị của $f(x)$ ta thấy không có giá trị nào làm cho $f(x)=0$ hoặc đổi dấu. Điều này có nghĩa $x=0$ là nghiệm duy nhất của phương trình.
Vậy phương trình có 1 nghiệm là $x=0$ chọn B
Cách 2: Tự Luận
$6.4^x-2.6^{x+1}+6.9^x=0$.
$\Leftrightarrow6.4^x-2.6^{x}.6^1+6.9^x=0$
$\Leftrightarrow6.4^x-12.6^{x}+6.9^x=0$
Vì $9^x>0$ nên ta chia 2 vế cho $9^x$
Phương trình đã cho
$\Leftrightarrow 6.\frac{4^x}{9^x}-12.\frac{6^{x}}{9^x}+6=0$
$\Leftrightarrow 6.\begin{bmatrix}\begin{pmatrix}\frac{2}{3}\end{pmatrix}^{x}\end{bmatrix}^{2}-12\begin{pmatrix}\frac{2}{3}
\end{pmatrix}^{x}+6=0$
Đặt $t=\begin{pmatrix}\frac{2}{3}\end{pmatrix}^{x}$ phương trình $\Leftrightarrow 6t^{2}-12t+6=0\Leftrightarrow t=1$
Vậy $\begin{pmatrix}\frac{2}{3}\end{pmatrix}^{x}=1 \Leftrightarrow x=0$
Kết Luận:
– Để sử dụng phương pháp Casio mà không bị sót nghiệm ta có thể sử dụng vài thiết lập miền giá trị của $x$ để kiểm tra.
– Theo cách tự luận ta quan sát thấy các số dạng đều có dạng bậc $2$. Vậy ta biết đây là phương trình dạng đẳng cấp bậc 2.
– Dạng phương trình đẳng cấp bậc 2 là phương trình có dang: $ma^2+nab+pb^2=0$ ta giải bằng cách chia 2 về cho $b^2$ rồi đặt ẩn phụ $\dfrac{a}{b}=t$.
About Toanbitexdtgd1
