BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Bài toán về phép giải tam giác trong bài thi HSG MTCT cấp THCS
- 30/09/2021
- 979 lượt xem
Tháng 1/2021 kỳ thi HSG MTCT do SGD và ĐT TP HCM tổ chức tiếp tục được duy trì. Để giúp các thầy cô phụ trách đội tuyển có thêm tài liệu tham khảo để bồi dưỡng đội tuyển, chúng tôi giới các đề thi gần đây của SGD và ĐT TP HCM.
|
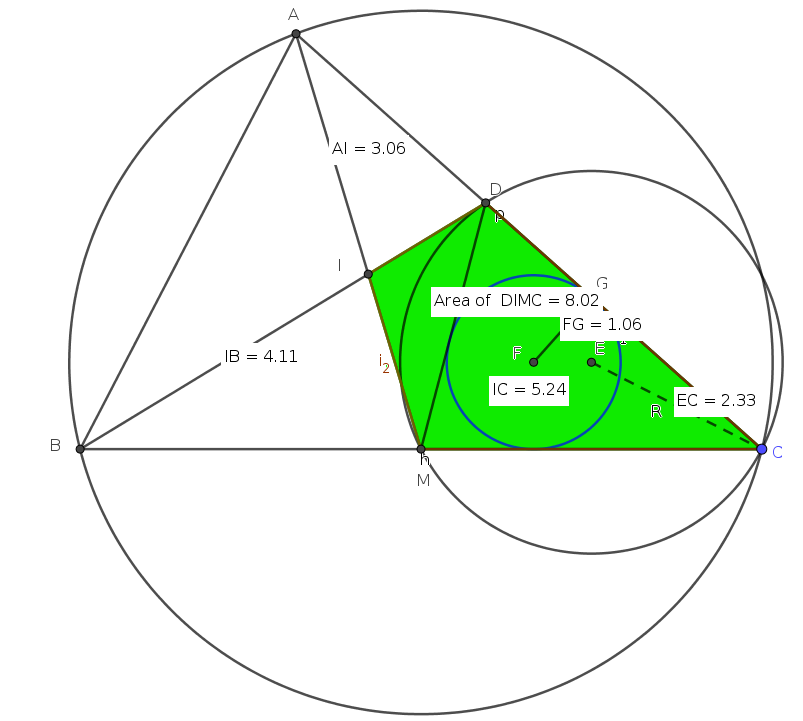
Bài 9. Cho tam giác ABC có cạnh $AB = 5,7; BC = 8,3; CA = 7,6$. Đường trung tuyến $AM$ cắt phân giác $BD$ tại $I$. Tính (chính xác đến 2 chữ số thập phân):
|
1. Định lý Mê-nê-la-uýt
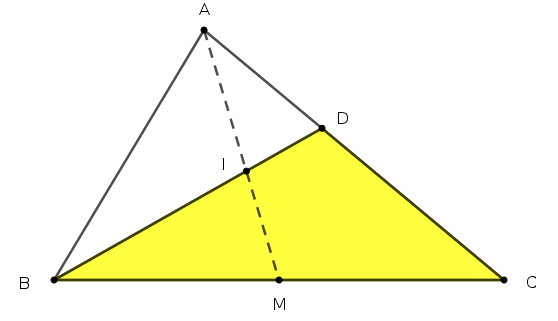
Áp dung định lý Mê-nê-la-uyt cho tam giác $BDC$ ta có: $$\dfrac{IB}{ID}\times \dfrac{AD}{AC}\times\dfrac{MC}{MB} =1$$
Cách nhớ định lý Mê-nê-la-uyt:
| $\dfrac{\quad B}{\quad\color{white}D}\times \dfrac{\quad D}{\quad\color{white}C}\times\dfrac{\quad C}{\quad\color{white}B} =1$
$\dfrac{IB}{\color{white}ID}\times \dfrac{AD}{\color{white}AC}\times\dfrac{MC}{\color{white}MB} =1$
|
Cụ thể với bài toán đã cho ta có:
$\dfrac{DA}{DC}=\dfrac{BA}{BC}$
$\Rightarrow \dfrac{AD}{AC}=$
.
$\Rightarrow \dfrac{IB}{ID}=$
.
Suy ra
$\dfrac{IB}{BD}=$
Tính được $IB$ dùng hệ thức hàm cos ta tính được $IA$ và $IC$.
2. Tính độ dài đường phân giác
Sử dụng lại hình vẽ ở trên, ta tính đoạn phân giác $BD$
Ta có: $S_{BAD}+S_{BDC}=S_{BAC}\Leftrightarrow \dfrac12.BA.BD.\sin\dfrac{B}{2}+\dfrac12.BD.BC.\sin\dfrac{B}{2}=\dfrac12.BA.BC.\sin B$
Trong khuôn khổ lớp 9 (HSG MT) ta có công thức (ghi nhớ):
| $$BD=\dfrac{BA.BC.\sin B}{(BA+BC)\sin\dfrac{B}{2}}$$ |
trong đó góc $B$ được tính bởi công thức:
| $$B=\arccos\dfrac{BA^2+BC^2-AC^2}{2BA.BC}$$ |
$\widehat{B}=$ 
lưu vào B.
$BD=$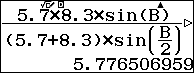 
lưu vào F.
$IB=$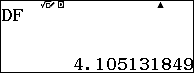
$IA=$ 
$IC=$
3. Tính bán kính của đường tròn ngoại tiếp tam giác $CDM$.
$DM=\sqrt{BD^2+BM^2-2.BD.BM.\cos \dfrac{B}{2}}$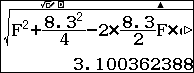
lưu vào D.
$\widehat{C}=$
lưu vào C.
Bán kính đường tròn ngoại tiếp tam giác $CDM$ là
$R=\dfrac{DM}{2\sin C}$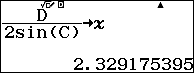 
lưu vào x.
4. Tính bán kính của đường tròn nội tiếp tam giác $CDM$.
$CD=$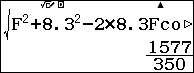
lưu vào y.
$r=\dfrac{S}{p}=\dfrac{abc}{2R(a+b+c)}$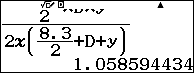 
5. Diện tích tứ giác $CDMI$.
$$S_{CDMI}=S_{BCD}-S_{BMI}=S_{BCD}.\left(1-\dfrac{BI}{BD}\times \dfrac{BM}{BC}\right)$$
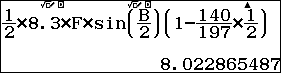
Đáp án: Vì không có sẵn đáp án của đề thi nên chúng tôi dùng geogebra để vẽ hình và xuất ra đáp án sau đây để đối chiếu với kết quả tính toán. Theo yêu cầu của bài toán đáp số viết dưới dạng số thập phân với hai số lẻ thập phân sau dấu phẩy
About TS. Nguyễn Thái Sơn
