BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
TỐC ĐỘ XỬ LÝ CỦA CASIO FX 580VNX THỂ HIỆN NHƯ THẾ NÀO TRONG BÀI TOÁN TÍNH TỔNG?
- 27/09/2021
- 2,383 lượt xem
Máy tính CASIO fx 580VNX được trang bị một sức mạnh xử lý vượt trội hơn so với dòng máy tính trước đó. Chúng ta cùng khám phá tốc độ tính toán của máy qua bài toán sau:
Bài toán tính tổng: Gọi $latex {{x}_{0}}$ là một nghiệm của phương trình $latex \sin 2x=\cos x$ trên $latex \left( \dfrac{\pi }{2};\pi \right)$. Tính giá trị của biểu thức $latex S=\sin {{x}_{0}}+\sin 2{{x}_{0}}+\sin 3{{x}_{0}}+…+\sin 2018{{x}_{0}}$
(Trích đề thi thử THPTQG năm 2018 cụm Sóc Sơn, Hà Nội) |
Lời giải tự luận:
Đầu tiên ta phải tìm nghiệm của phương trình $latex \sin 2x=\cos x$ trên $\left( \dfrac{\pi }{2};\pi \right)$.Ta có:
$latex \sin 2x=\cos x\Leftrightarrow 2\sin x\cos x=\cos x\Leftrightarrow 2\sin x=1$ (do $latex \cos x\ne 0$ $\forall x\in \left( \dfrac{\pi }{2};\pi \right)$)
Do đó $latex \sin x=\dfrac{1}{2}\Rightarrow {{x}_{0}}=\dfrac{5\pi }{6}$ (do $latex x\in \left( \dfrac{\pi }{2};\pi \right)$)
Để tính được tổng $latex (S)$ ta có công thức sau:
$latex \sin x+\sin 2x+…\sin nx=\dfrac{\cos \dfrac{x}{2}-\cos \left( \left(n+\dfrac{1}{2} \right)x \right)}{2\sin \dfrac{x}{2}}$ (1)
(Chứng minh công thức ở phía cuối bài viết)
Áp dụng công thức trên với $latex n=2018$ và ${{x}_{0}}=\dfrac{5\pi }{6}$ ta có:
$latex \begin{align} & S=\sin {{x}_{0}}+\sin 2{{x}_{0}}+…+\sin 2018{{x}_{0}}=\dfrac{\cos \dfrac{{{x}_{0}}}{2}-\cos \left(\left( 2018+\dfrac{1}{2} \right){{x}_{0}}\right)}{2\sin \dfrac{{{x}_{0}}}{2}} \\ & =\dfrac{1}{2}\left( \cot \dfrac{5\pi }{12}-\dfrac{\cos \left( \dfrac{\pi }{12} \right)}{\sin \left( \dfrac{5\pi }{12} \right)} \right) \\ & =\dfrac{1}{2}\left( \cot \dfrac{5\pi }{12}-1 \right) \\ & =\dfrac{1-\sqrt{3}}{2} \end{align}$
Vậy ta chọn đáp án A.
Nhận xét: rõ ràng lời giải bài toán này không dễ nếu chúng ta không biết đến công thức trên. Do đó việc dùng máy tính hỗ trợ tìm đáp án sẽ là lựa chọn tốt. Để giải bài toán tính tổng này ta thao tác như sau:
Bước 1: Chuyển máy tính sang chế độ Radian:
- Cách bấm: qw22
- Máy tính hiển thị:
Bước 2: Nhập biểu thức $latex \sum\limits_{x = 1}^{2018} {\left( {\sin \left( {\frac{{5\pi }}{6}x} \right)} \right)}$:
- Cách bấm: q[jQ(Oa5qKR6$)R1E2018
- Máy tính hiển thị:
Bước 3: Nhấn phím = và chờ máy trả kết quả
Bước 4: Lưu kết quả vừa tính vào biến A:
- Cách bấm: Jz
- Máy tính hiển thị:
Bước 5: Kiểm tra đáp án:
- Cách bấm máy tính: Qzpa1ps3R2=
- Máy tính hiển thị:
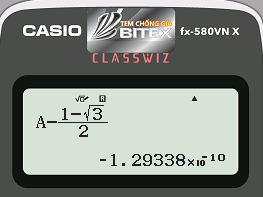
Kết quả $latex A-\dfrac{1-\sqrt{3}}{2}\approx 0$ nên ta chọn đáp án A.
Trước khi trình bày chứng minh của công thức (1), tác giả muốn nhấn mạnh rằng việc tính toán tổng $latex \sum\limits_{x=1}^{2018}{\left( \dfrac{5\pi }{6}x \right)}$ ra kết quả nhanh hay chậm tuỳ vào sức mạnh tính toán của máy tính cầm tay, với tốc độ tính toán được cải tiến rất nhiều, so sánh với máy tính CASIO fx570VN Plus, ta có kết quả sau:
Chứng minh công thức (1):
Ta sẽ chứng minh công thức trên bằng quy nạp.
Với $latex n=1$ ta có: $latex (1)\Leftrightarrow \sin x=\frac{\cos \dfrac{x}{2}-\cos \frac{3x}{2}}{2\sin \frac{x}{2}}=\frac{-2\sin \left( \frac{1}{2}\left( \frac{x}{2}+\frac{3x}{2} \right) \right)\sin \left( \frac{1}{2}\left( \frac{x}{2}-\frac{3x}{2} \right) \right)}{2\sin \frac{x}{2}}$
$latex =\frac{-2\sin \left( \frac{x}{2} \right)\sin \left( \frac{-x}{2} \right)}{2\sin \frac{x}{2}}=\sin x$. Vậy (1) đúng với $latex n=1$.
Giả sử (1) đúng với $latex n=k\ge 1$. Xét $latex n=k+1$ ta có:
$latex \sin x+\sin 2x+…\sin nx+\sin (n+1)x=\frac{\cos \frac{x}{2}-\cos \left( n+\frac{1}{2} \right)x}{2\sin \frac{x}{2}}+\sin (n+1)x$
$latex \begin{align} & =\frac{\cos \frac{x}{2}-\cos \left( n+\frac{1}{2} \right)x}{2\sin \frac{x}{2}}+\frac{2\sin (n+1)x.\sin \frac{x}{2}}{2\sin \frac{x}{2}} \\ & =\frac{\cos \frac{x}{2}-\cos \left( n+\frac{1}{2} \right)x}{2\sin \frac{x}{2}}-\frac{\cos \left( (n+1)x+\frac{x}{2} \right)-\cos \left( (n+1)x-\frac{x}{2} \right)}{2\sin \frac{x}{2}} \\ & =\frac{\cos \frac{x}{2}-\cos \left( n+\frac{1}{2} \right)x}{2\sin \frac{x}{2}}-\frac{\cos \left( n+1+\frac{1}{2} \right)x-\cos \left( n+\frac{1}{2} \right)x}{2\sin \frac{x}{2}} \\ & =\frac{\cos \frac{x}{2}-\cos \left( n+1+\frac{1}{2} \right)x}{2\sin \frac{x}{2}}\\ \end{align}$
Vậy (1) đúng với $latex n=k+1$, do đó theo phép quy nạp toán học ta đã chứng minh công thức trên là đúng.
About TailieuCasio
