BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG PHƯƠNG PHÁP NÂNG LŨY THỪA VÀ ĐỊNH LÝ VIET ĐẢO ĐỂ GIẢI PHƯƠNG TRÌNH
- 29/06/2022
- 572 lượt xem
Phương trình chứa căn hay còn gọi là phương trình vô tỷ là một bài toán thường gặp trong chương trình phổ thông và gây rất nhiều khó khăn cho học sinh trong quá trình làm bài. Trong
Cơ sở lý thuyết
Nếu một đa thức $P\left( x \right)$ có các nghiệm phân biệt ${{x}_{1}},{{x}_{2}}$ và $S={{x}_{1}}+{{x}_{2}}$, $P={{x}_{1}}{{x}_{2}}$ thì đa thức $P\left( x \right)$ chia hết cho ${{x}^{2}}-Sx+P$
Nếu chia $P\left( x \right)$ cho ${{x}^{2}}-Sx+P$ ra $Q\left( x \right)$ thì ta có $P\left( x \right)=Q\left( x \right)\left( {{x}^{2}}-Sx+P \right)$
Bài toán 1. Giải phương trình ${{x}^{2}}-3x-2=\left( x-1 \right)\sqrt{2x+1}$
Hướng dẫn giải
Điều kiện: $\left\{ \begin{align} & 2x+1\ge 0 \\ & \left( {{x}^{2}}-3x-2 \right)\left( x-1 \right)\ge 0 \\\end{align} \right.$ $ \Leftrightarrow \left[ \begin{align} & 1\ge x\ge \dfrac{-1}{2} \\& x\ge \dfrac{3+\sqrt{17}}{2} \\\end{align} \right.$
Bình phương hai vế của phương trình ta có:
${{\left( {{x}^{2}}-3x-2 \right)}^{2}}={{\left( x-1 \right)}^{2}}\left( 2x+1 \right)$ $ \Leftrightarrow {{\left( {{x}^{2}}-3x-2 \right)}^{2}}-{{\left( x-1 \right)}^{2}}\left( 2x+1 \right)=0\\$
Thay $x=100$ vào vế trái của phương trình ta có:
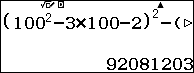
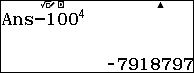
${{\left( {{x}^{2}}-3x-2 \right)}^{2}}-{{\left( x-1 \right)}^{2}}\left( 2x-1 \right)=92081203=100000000-7918797\\$
Phân tích:
- $100000000={{x}^{4}}\\$
- $7918797\to 7\sim 91\sim 87\sim 97$ $latex \to 7\sim \left( 100-9 \right)\sim \left( 100-13 \right)\sim \left( 100-3 \right)$
Suy ra:
${{\left( {{x}^{2}}-3x-2 \right)}^{2}}-{{\left( x-1 \right)}^{2}}\left( 2x+1 \right)\\$
$={{x}^{4}}-\left[ 7{{x}^{3}}+\left( x-9 \right){{x}^{2}}+\left( x-13 \right)x+\left( x-3 \right) \right]\\$
$={{x}^{4}}-8{{x}^{3}}+8{{x}^{2}}+12x+3\\$
Như vậy phương trình đã cho tương đương với phương trình: ${{x}^{4}}-8{{x}^{3}}+8{{x}^{2}}+12x+3=0$
Sử dụng máy tính Casio fx 580 VNX để giải phương trình bậc 4
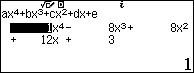
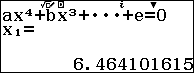
So lại điều kiện ta loại 2 nghiệm ${{x}_{2}}$, ${{x}_{3}}$ và nhận ${{x}_{1}},{{x}_{4}}$
Do nghiệm của phương trình bậc 4 này ở dạng số thập phân khá phức tạp nên ta sẽ sử dụng định lý Viet đảo để tìm nghiệm của hai phương trình bậc 2.
Lưu lại 2 nghiệm ${{x}_{1}},{{x}_{4}}$ của phương trình bậc 4 trên vào các ô nhớ $A$và $D$
Như vậy ta có: ${{x}_{1}},{{x}_{4}}$ là nghiệm của phương trình ${{x}^{2}}-6x-3=0$
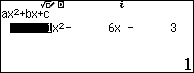
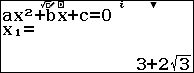
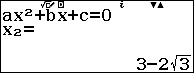
Vậy nghiệm của phương trình đã cho là ${{x}_{1}}=3+2\sqrt{3}$và ${{x}_{2}}=3-2\sqrt{3}$
Bài toán 2. Giải phương trình ${{x}^{2}}-6x-2=\sqrt{x+8}$
Hướng dẫn giải
Điều kiện:$\left\{ \begin{align} & x+8\ge 0 \\& {{x}^{2}}-6x-2\ge 0 \\\end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& x\ge -8 \\& x\ge 3+\sqrt{11}\vee x\le 3-\sqrt{11} \\\end{align} \right.$ $\Leftrightarrow \left[ \begin{align} & -8\le x\le 3-\sqrt{11} \\ & x\ge 3+\sqrt{11} \\\end{align} \right.$
Bình phương hai vế phương trình ta được: ${{\left( {{x}^{2}}-6x-2 \right)}^{2}}=x+8$
Thay $x=100$ vào ${{\left( {{x}^{2}}-6x-2 \right)}^{2}}$ ta được: ${{\left( {{x}^{2}}-6x-2 \right)}^{2}}$$=88311404={{100}^{4}}-11677596$
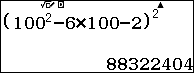
Phân tích: $11677596\to 11\sim 67\sim 75\sim 96\to 11\sim \left( x-33 \right)\sim \left( x-25 \right)\sim \left( x-4 \right)$
Như vậy :
${{\left( {{x}^{2}}-6x-2 \right)}^{2}}=x+8\\$
$\Leftrightarrow {{x}^{4}}-\left[ 11{{x}^{3}}+\left( x-33 \right){{x}^{2}}+\left( x-25 \right)x+\left( x-4 \right) \right]=x+8\\$
$\Leftrightarrow {{x}^{4}}-12{{x}^{3}}+32{{x}^{2}}+23x-4=0\\$
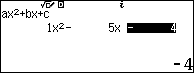
Sử dụng máy tính Casio fx 580 vnx để giải và lưu lần lượt các nghiệm của phương trình bậc $4$ trên vào các ô nhớ $A, B, C$ và $D$
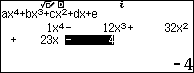
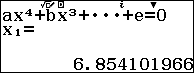
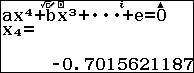
Dựa vào kết quả các nghiệm ta sẽ tính các tổng và tích
Như vậy ${{x}_{1}},{{x}_{3}}$ là nghiệm của phương trình ${{x}^{2}}-7x+1=0$ và ${{x}_{2}},{{x}_{4}}$ là nghiệm của phương trình ${{x}^{2}}-5x-4=0$
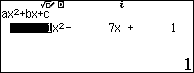
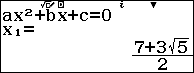
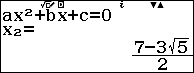
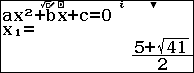
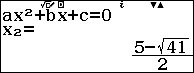
So lại điều kiện, phương trình đã cho có $2$ nghiệm phân biệt $x=\dfrac{7+3\sqrt{5}}{2}$ và $x=\dfrac{5-\sqrt{41}}{2}$
Bài toán 3. Giải phương trình $3{{x}^{2}}=\sqrt[3]{{{x}^{3}}+4x+2}$
Hướng dẫn giải
Ta có: $3{{x}^{2}}=\sqrt[3]{{{x}^{3}}+4x+2}$ $\Leftrightarrow 27{{x}^{6}}={{x}^{3}}+4x+2$ $\Leftrightarrow 27{{x}^{6}}-{{x}^{3}}-4x-2=0$
Sử dụng qr(SOLVE) để dò nghiệm phương trình trên và lưu nghiệm vào ô nhớ $A$ và $B$
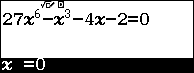
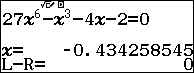
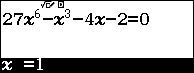
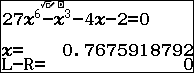
Tính tổng và tích của hai nghiệm trên
Như vậy hai nghiệm trên cũng là nghiệm của phương trình ${{x}^{2}}-\dfrac{1}{3}x-\dfrac{1}{3}=0$
Suy ra $27{{x}^{6}}-{{x}^{3}}-4x-2=\left( {{x}^{2}}-\dfrac{x}{3}-\dfrac{1}{3} \right)Q\left( x \right)$
$\Rightarrow Q\left( x \right)=\dfrac{27{{x}^{6}}-{{x}^{3}}-4x-2}{{{x}^{2}}-\dfrac{x}{3}-\dfrac{1}{3}}$
Thay $x=100$ vào biểu thức ta có $Q\left( 100 \right)=2709120606\to 27-09-12-06-06$
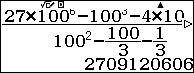
$\to Q\left( x \right)=27{{x}^{4}}+9{{x}^{3}}+12{{x}^{2}}+6x+6$
Suy ra $27{{x}^{6}}-{{x}^{3}}-4x-2$$=\left( {{x}^{2}}-\dfrac{x}{3}-\dfrac{1}{3} \right)\left( 27{{x}^{4}}+9{{x}^{3}}+12{{x}^{2}}+6x+6 \right)$
Ta có: $Q\left( x \right)=27{{x}^{4}}+9{{x}^{3}}+12{{x}^{2}}+6x+6$ $=3{{x}^{2}}\left( 9{{x}^{2}}+3x+1 \right)+\left( 9{{x}^{2}}+6x+1 \right)+5$ $x >0\forall x\in \mathbb{R}$
Như vậy nghiệm của bài toán là nghiệm của phương trình ${{x}^{2}}-\dfrac{1}{3}x-\dfrac{1}{3}=0$
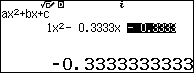
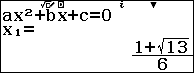
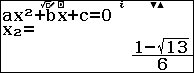
So với điều kiện ban đầu ta có nghiệm của phương trình đã cho là $x=\dfrac{1\pm \sqrt{13}}{6}$
Cảm ơn các bạn đã theo dõi bài viết SỬ DỤNG PHƯƠNG PHÁP NÂNG LŨY THỪA VÀ ĐỊNH LÝ VIET ĐẢO ĐỂ GIẢI PHƯƠNG TRÌNH . Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
