Một áp dụng của Định lý Mê-nê-la-uýt
- 29/06/2022
- 1,076 lượt xem
|
Cho tam giác $ABC$. Trên các đoạn $CA$ và $CB$ ta lấy các điểm $D$ và $M$ tương ứng sao cho $\dfrac{CD}{CA}=a\ ; \ \dfrac{CM}{CB}=b$.Tính các tỉ số $\dfrac{AI}{AM}$ và $\dfrac{BI}{BD}$. |
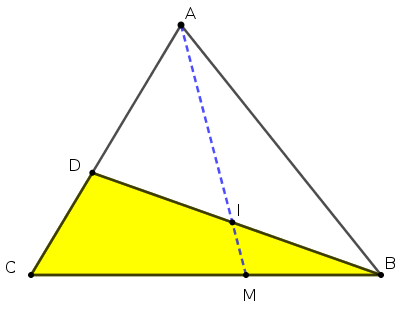
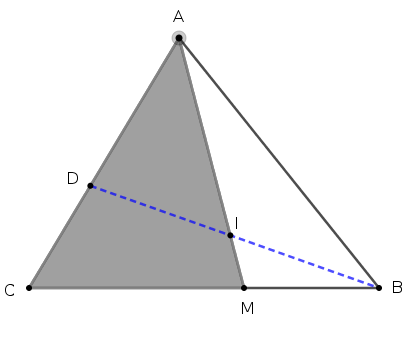
Áp dụng Định lý Mê-nê-la-uýt cho tam giác $BCD$ với cát tuyến $AIM$ ta có:
$$\dfrac{MB}{MC}\times\dfrac{AC}{AD}\times\dfrac{ID}{IB}=1$$
Theo giả thiết ta có:
$\left.\begin{array}{l}\dfrac{CD}{CA}=a\Rightarrow \dfrac{AC}{AD}=\dfrac{1}{1-a}\\ \dfrac{CM}{CB}=b\Rightarrow \dfrac{MB}{MC}=\dfrac{1-b}{b}\end{array}\right\} \Rightarrow \dfrac{ID}{IB}= \dfrac{b-ba}{1-b}$
Vậy
| $\qquad \qquad\qquad\qquad \qquad\qquad\dfrac{BI}{BD}=\dfrac{1-b}{1-ab}$ |
Tính toán tương tự
| $\qquad \qquad\qquad\qquad \qquad\qquad\dfrac{AI}{AM}=\dfrac{1-a}{1-ab}$ |
Áp dụng: Cho tam giác ABC có cạnh $AB=5,7;BC=8,3;CA=7,6$. Đường trung tuyến $AM$ cắt phân giác $BD$ tại $I$.
Ta có:
$b=\dfrac{CM}{CB}=\dfrac12$
$\dfrac{DC}{DA}=\dfrac{BC}{BA}=\dfrac{83}{57}\Rightarrow a=\dfrac{CD}{CA}=$
Vậy $\dfrac{BI}{BD}=$
$\dfrac{AI}{AM}=$
Trong bài trước ta tính $AI$ dựa vào hệ thức hàm cos (công thức không dành cho HS lớp 9 PT, nhưng dành cho HS lớp 9 giỏi MTCT). Trong bài này ta tính $AI$ dựa vào hệ thức tính trung tuyến $AM^2=\dfrac{AB^2+AC^2-\dfrac{BC^2}{2}}{2}$
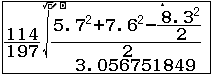
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay