MỘT SỐ BÀI TOÁN NÓN TRỤ CẦU ÔN THI VÀO LỚP 10

12/05/2021
1,370 lượt xem
Toanbitexdtgd

Bài 1: Một chiếc thùng chứa đầy nước có hình một khối lập phương. Đặt vào trong thùng đó một khối nón sao cho đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước trào ra ngoài và lượng nước còn lại ở trong thùng.

Hướng dẫn:

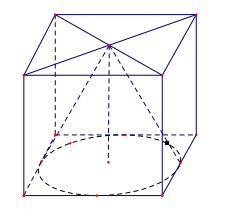
Coi khối lập phương có cạnh 1. Thể tích khối lập phương là V=1.

Từ giả thiết ta suy ra khối nón có chiều cao h=1, bán kính đáy $r=\frac{1}{2}$ .

Thể tích lượng nước trào ra ngoài là thể tích $V_{1}$ của khối nón.

Ta có: $V_{1}=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi .\frac{1}{4}.1=\frac{\pi }{12}$ .

Thể tích lượng nước còn lại trong thùng là: $V_{2}=V-V_{1}=1-\frac{\pi }{12}=\frac{12-\pi }{12}.$

Do đó: $\frac{V_{1}}{V_{2}}=\frac{\pi }{12-\pi }.$

Bài 2: Trong một chiếc hộp hình trụ, người ta bỏ vào đấy ba quả banh tenis, biết rằng đáy của hình trụ bằng hình tròn lớn trên quả banh và chiều cao của hình trụ bằng ba lần đường kính của quả banh, Gọi $S_{1}$ là tổng diện tích của ba quả banh, $S_{2}$ là diện tích xung quanh của hình trụ. Tính tỉ số diện tích $\frac{S_{1}}{S_{2}}$ .

Hướng dẫn:

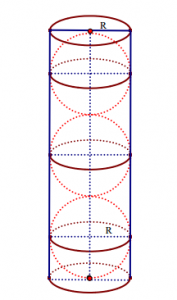
Gọi bán kính của đường tròn lớn quả banh tenis là R.

Diện tích của một quả banh tenis là $4\pi R^{2}$ .

Suy ra $S_{1}=12\pi R^{2}$ .

Chiều cao của chiếc hộp hình trụ là 6R.

Diện tích xung quanh của hình trụ là $S_{2}=2\pi R.6R=12\pi R^{2}.$

Do đó $\frac{S_{1}}{S_{2}}=1$

Bài 3: Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1, chiều cao bằng 2. Người ta khoét từ hai đầu khối gỗ hai nửa khối cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu. Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu

Hướng dẫn:

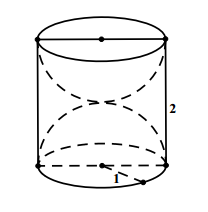Thể tích của khối trụ là $V=\pi .1^{2}.2=2\pi$

Vì đường tròn đáy của khối trụ là đường tròn lớn của mỗi nửa khổi cầu nên bán kính của mỗi nửa khối cầu là R=1.

Thể tích của hai nửa khối cầu bị khoét đi là $V_{1}=2.\frac{1}{2}\frac{4\pi .1^{3}}{3}=\frac{4\pi }{3}.$

Thể tích của phần còn lại của khối gỗ là $V_{2}=V-V_{1}=2\pi -\frac{4\pi }{3}=\frac{2\pi }{3}$

Vậy tỉ số thể tích cần tìm là $\frac{V_{2}}{V}=\frac{\frac{2\pi }{3}}{2\pi }=\frac{1}{3}$

Bài 4: Lượng nguyên liệu cần dùng để làm ra một chiếc nón lá được ước lượng qua phép tính diện tích xung quanh của mặt nón. Cứ 1kg lá dùng để làm nón có thể làm ra số nón có tổng diện tích xung quanh là $6,13m^{2}$ . Hỏi nếu muốn làm ra 1000 chiếc nón lá giống nhau có đường trình vành nón 50cm, chiều cao 30cm thì cần khối lượng bao nhiêu (coi mỗi chiếc nón có hình dạng là một hình nón)
Hướng dẫn:

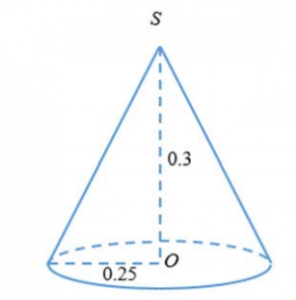
Theo giả thiết mỗi chiếc nón lá là một hình nón có bán kính đáy $R=\frac{50}{2}=25(cm)=0,25(m)$ và đường cao $h=30(cm)=0,3(m)$

Gọi l là chiều cao của hình nón $\Rightarrow l=\sqrt{R^{2}+h^{2}}=\frac{\sqrt{61}}{20}(m)$

Diện tích xung quanh của 1 chiếc nón lá là $S_{xq}=\pi Rl=\pi .0,25.\frac{\sqrt{61}}{20}=\frac{\pi \sqrt{61}}{80}(m^{2})$

Tổng diện tích xung quanh của 1000 chiếc nón là $S=1000.\frac{\pi \sqrt{61}}{80}=\frac{25\pi \sqrt{61}}{2}(m^{2})$

Do đó khối lượng lá cần dùng là $\frac{S}{6,13}\approx 50,03(kg)$

Bài 5: Một khối đồ chơi gồm hai khối cầu $(H_{1}),(H_{2})$ tiếp xúc với nhau, lần lượt có bán kính tương ứng là $r_{1},r_{2}$ thỏa mãn $r_{2}=\frac{1}{2}r_{1}$ . biết rằng thể tích của toán bộ khối đồ chơi bằng $180cm^{3}$ . Tính thề tích của khối cầu $(H_{1})$

Hướng dẫn:

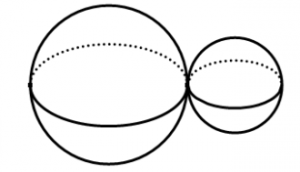
Thể tích khối $(H_{1})$ là $V_{1}=\frac{4}{3}\pi r_{1}^{3}$

Thể tích khối $(H_{2})$ là $V_{2}=\frac{4}{3}\pi r_{2}^{3}$

Tổng thể tích 2 khối là

$V=V_{1}+V_{2}=\frac{4}{3}\pi r_{1}^{3}+\frac{4}{3}\pi r_{2}^{3}=\frac{4}{3}\pi r_{1}^{3}+\frac{4}{3}\pi \left ( \frac{1}{2} r_{1}\right )^{3}=\frac{9}{8}.\frac{4}{3}\pi r_{1}^{3}=\frac{9}{8}V_{1}$

Suy ra $\frac{9}{8}V_{1}=180\Rightarrow V_{1}=160$

Từ khóa:

#nón trụ cầu

Chia sẻ

H	B	T	N	S	B	C
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay

MỘT SỐ BÀI TOÁN NÓN TRỤ CẦU ÔN THI VÀO LỚP 10

About Bitex Khánh Vũ

Bài viết liên quan

Bài Viết Tương Tự

SỬ DỤNG MÁY TÍNH FX-880BTG KIỂM TRA SỐ NGUYÊN TỐ

BẢN TIN

ĐĂNG KÝ NHẬN BẢN TIN