Đặc điểm của khối tứ diện khi biết trước độ dài của 6 cạnh
- 20/12/2021
- 440 lượt xem
Đặt vấn đề: Khi ta gặp một khối tứ diện với độ dài 6 cạnh không có tính chất gì đặc biệt (chẳng hạn không có ba cạnh nào bằng nhau mà cùng đi qua 1 đỉnh, không có cạnh nào vuông góc với mặt phẳng đi qua 3 đỉnh còn lại v.v…) thì ta có các công thức hữu ích sau đây để trả lời câu trắc nghiệm VDC (thường là từ câu 45 -50).
- Thể tích $V$ của khối tứ diện đó.
- Bán kính mặt cầu ngoại tiếp khối tứ diện đó.
- Góc tạo bởi hai cạnh đối diện.
- Khoảng cách ngắn nhất của hai cạnh đối diện.
Các công thức 1 và 2 chúng tôi đã trình bày nhiều lần, chẳng hạn trong quyển sách “Giải nhanh bài thi trắc nghiệm môn Toán trên MTCT Casio fx-580 VNX”. Trên diễn đàn này chúng tôi giới thiệu và chứng minh hai công thức còn lại.
3) Góc tạo bởi hai cạnh AB và CD
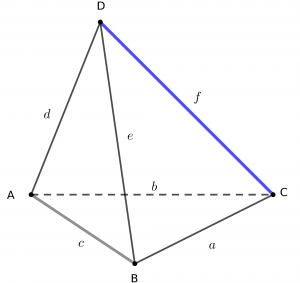
$\cos (\overrightarrow{AB},\overrightarrow{CD})=\dfrac{\overrightarrow{AB}.\overrightarrow{CD}}{AB.CD}=\dfrac{(\overrightarrow{AD}-\overrightarrow{CD}+\overrightarrow{CB}).\overrightarrow{CD}}{cf}$
$=\dfrac{\overrightarrow{AD}.\overrightarrow{CD}-\left(\overrightarrow{CD}\right)^2+\overrightarrow{CB}.\overrightarrow{CD}}{cf}=\dfrac{d^2+f^2-b^2-2f^2+f^2+a^2-e^2}{2cf}$
Vậy:
| $$\cos(AB,CD)=\dfrac{\left|a^2+d^2-b^2-e^2\right|}{2cf}$$ |
4) Khoảng cách $d(AB,CD)$
Áp dụng công thức tính thế tích
$$V_{ABCD}=\dfrac16.AB.CD.d(AB,CD).\sin (AB,CD)$$
Suy ra
| $$d(AB,CD)=\dfrac{6V_{ABCD}}{AB.CD.\sin(AB,CD)}=\dfrac{12V_{ABCD}}{\sqrt{4c^2f^2-(a^2+d^2-b^2-e^2)^2}}$$ |

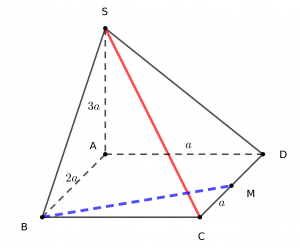
Đây là đề thi thử Chuyên Vinh lần 3 năm 2019
Giải:
Ngoài phương pháp truyền thống:
- Đo độ dài đoạn vuông góc chung
- Tính khoảng cách từ 1 điểm trên đường thẳng này đến mặt phẳng chứa đường thẳng kia và có cặp vectơ chỉ phương là các vectơ chỉ phương của hai đường thẳng
- Dùng tích hỗn tạp và độ dài của tích có hướng
Hôm nay ta biết thêm một cách nữa đó là xét tứ diện $SBCM$ với 6 cạnh như sau:
- $SC=\sqrt{14}a, BM=\sqrt2 a$
- $SB=\sqrt{13}a, CM=a$
- $SM=\sqrt{11}a, BC=a$
Áp dung công thức vừa chứng minh, thao tác trên MTCT Casio fx-580 VNX ta có:
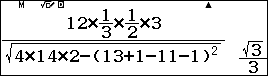
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay