BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI BÀI TOÁN TIỆM CẬN CÓ THAM SỐ TRÊN MÁY TÍNH CẦM TAY CASIO FX 580VNX
- 06/09/2018
- 1,182 lượt xem
Bài toán: Cho hàm số $latex y=\dfrac{mx-3}{x-2}$ $({{C}_{m}})$. Tìm $latex m$ để giao điểm của hai tiệm cận của $latex ({{C}_{m}})$ trùng với toạ độ điểm cực tiểu của đồ thị hàm số $latex y={{x}^{3}}-3{{x}^{2}}+2$.
|
Lời giải:
Tập xác định của hàm số $latex D=\mathbb{R}\backslash \{2\}$
Giao điểm của hai tiệm cận của $latex ({{C}_{m}})$ là $M(2;m)$.
Ta tìm toạ độ điểm cực tiểu của đồ thị hàm số $latex y={{x}^{3}}-3{{x}^{2}}+2$ bằng máy tính cầm tay CASIO fx 580VNX như sau:
Bước 1: Mở chức năng giải phương trình bậc 3
- Cách bấm máy tính CASIO fx 580VNX: w923
- Máy tính CASIO fx 580VNX hiển thị:
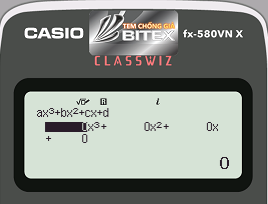
Bước 2: Nhập hệ số của hàm số
- Cách bấm máy tính CASIO fx 580VNX: ==0=2=2P29=
- Máy tính CASIO fx 580VNX hiển thị:
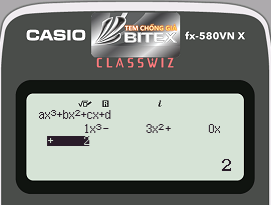
Bước 3: Nhấn phím = tới khi máy hiển thị giá trị của điểm cực tiểu
- Máy tính CASIO fx 580VNX hiển thị:
Vậy điểm cực tiểu của đồ thị hàm số $latex y={{x}^{3}}-3{{x}^{2}}+2$ là $A(2;-2)$, do đó để $latex M\equiv A$ thì $latex m=-2$.
Vậy ta chọn đáp án D
Chia sẻ
About Bitex Casio
