Ba cách tính khoảng cách giữa hai đường thẳng chéo nhau (1)

Giả sử ycbt  là tính d(AB, CD)

Cách 1:

• – Tìm một  mặt phẳng chứa $CD$ và song song với $AB$. Gọi mặt phẳng này là $\alpha$
• – $d(AB,CD)=d(AB,\alpha) =d(A,\alpha)$.
• – Giả sử có một đường thẳng  $d$ đi qua $A$ và song song với $\alpha$, trên đường thẳng  này chứa một điểm $H$ mà dễ tính $d(H,\alpha)$ thì
  $$d(H,\alpha)=d(A,\alpha)=d(AB,CD)$$
• – Muốn tính $d(H,\alpha)$ ta tìm một mặt phẳng $\beta$ đi qua $H$ và vuông góc với $\alpha$. Từ $H$ ta hạ $HK$ vuông góc với giao tuyến ta sẽ có $$HK=d(H,\alpha)$$

Ví dụ: Cho một hình hộp $ABCDA’B’C’D’$ có tất cả các cạnh đều bằng $1$ và các góc phẳng đỉnh $A$ đều bằng $60^\circ$. Tính $d(AB’, A’C’)$.

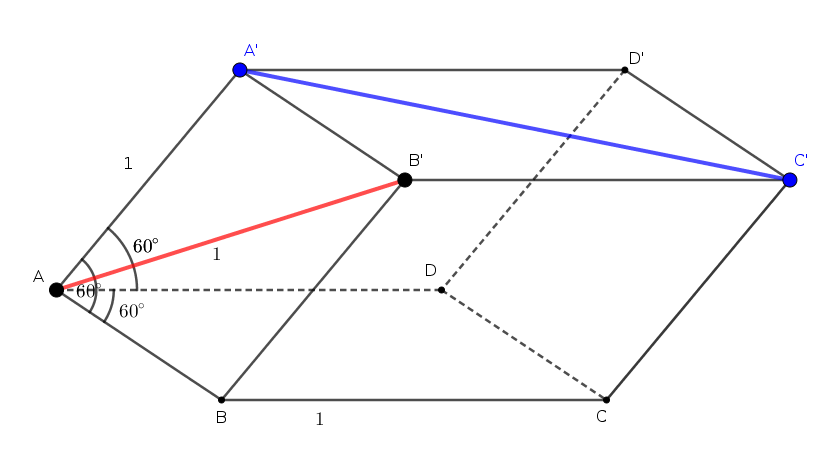
Giải:

Mặt phẳng $(DA’C’)$ chứa $A’C’$ và song song với $AB’$ nên $d(AB’,A’C’)=d(A,(DA’C’))$.

Vì $AC$ song song với $(DA’C’)$ nên $d(A,(DA’C’)$ sẽ bằng khoảng cách từ một điểm đặc biệt nào đó trên $AC$ đến $(DA’C’)$. Ta tìm điểm đó.

Nhận xét rằng $A’A=A’B=A’D$ nên hình chiếu vuông góc $H$ của $A’$ trên $(ABD)$ là tâm đường tròn ngoại tiếp tam giác $DAB$.

Ta có: $d(A, (DA’C’)=d(H,(DA’C’)$

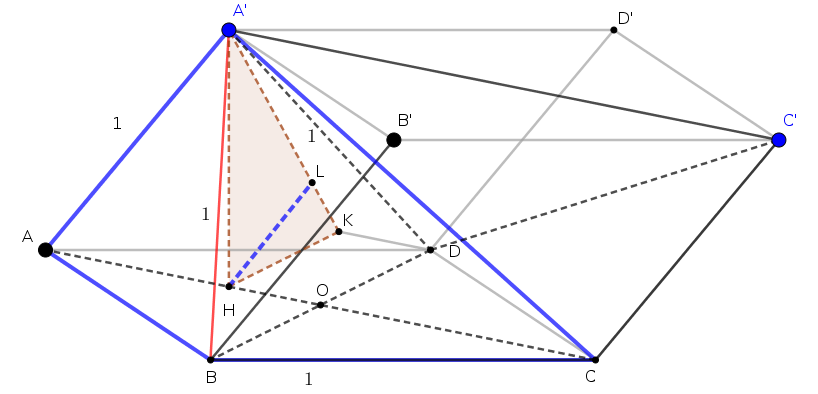
Trong mặt phẳng $(ABD)$ dựng hình bình hành $HODK$ ta thấy hình bình hành này trở thành hình chữ nhật (do $ABCD$ là hình thoi).

Nhận xét rằng $A’C’ // AC$ mà $AC\perp (A’HK)$ nên $A’C’ \perp (A’HK)$, suy ra $(A’HK) \perp (DA’C’)$ và cắt nhau theo giao tuyến $A’K$. Từ $H$ hạ $HL\perp A’K$ thì $HL\perp (DA’C’)$, nghĩa là $HL=d(H,(DA’C’)$.

$$\dfrac{1}{HL^2}=\dfrac{1}{HA’^2}+\dfrac{1}{HK^2}=\dfrac{1}{1^2-\left(\dfrac{\sqrt3}{3}\right)^2}+\dfrac{1}{\left(\dfrac12\right)^2}$$

Chú ý $BD=1$ và $AC=\sqrt3$.

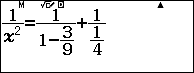
Tóm lại $d(AB’,A’C’)=\dfrac{\sqrt{22}}{11}$.

Nhận xét:  Để thực hiện được cách làm như trên học sinh phải rèn luyện thật là kỹ lưỡng kỹ năng tính khoảng cách trong HHKG, trong đó yếu tố tìm được điểm $H$ là rất cần thiết và đòi hỏi phải có năng lực thật sự về HHKG.

Một lời giải đầy kỹ thuật như vừa thực hiên ở trên sẽ chiếm khá nhiều thời gian trong 90 phút nên HS buộc phải làm những câu NB và TH thật nhanh mới có đủ thời gian làm câu VD và VDC như bài này.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.