ỨNG DỤNG CASIO FX-580VN X VÀO TÍNH ĐỘ LỚN, TÍCH VÔ HƯỚNG, TÍCH CÓ HƯỚNG CỦA VECTOR
- 11/04/2022
- 201 lượt xem
1. Cách nhập tọa độ của vector bằng Casio Fx-580VN X
Ví dụ: Nhập Vector $A(2;6)$ ta thực hiện như sau
Bước 1: Lựa chọn chức năng tính Vector
Thực hiện thao tác: w5
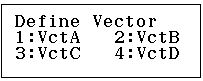
Lưu ý rằng màn hình lựa chọn vector cũng xuất hiện bất cứ khi nào bạn vào phương thức Vector.
Bước 2: Nhấn chọn số $1, 2, 3$ hoặc $4$ để chỉ định tên của Vector muốn chọn.

Bước 3: Nhấn chọn số $2$ hoặc $3$ để chỉ định chiều của Vector
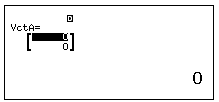
Bước 4: Nhập giá trị của Vector
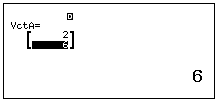
2. Tính tích vô hướng của $2$ Vector
$({a_1},{a_2})\times({b_1},{b_2})={a_1}{b_1}+{a_2}{b_2}$
$({a_1},{a_2},{a_3})\times({b_1},{b_2},{b_3})={a_1}{b_1}+{a_2}{b_2}+{a_3}{b_3}$
Ví dụ: Tính tích vô hướng của Vector $A(1;2)$ và Vector $B(-2;3)$
Nhập lần lượt các Vector vào máy:
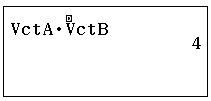
Ví dụ: Tính tích có hướng của Vector $A(1;2)$ và Vector $B(-2;3)$
Nhập lần lượt các Vector vào máy:
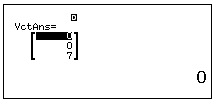
Nhập lần lượt các Vector vào máy:
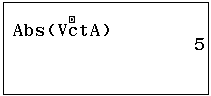
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay