BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BÀI TẬP XÁC SUẤT CỦA BIẾN CỐ
- 22/01/2022
- 549 lượt xem
Trong bài viết này, chúng tôi sẽ giới thiệu một số bài toán xác suất và sự hỗ trợ của máy tính Casio Fx-580VN X vào giải các bài toán đó.
Bài toán 1: Một hộp đựng $10$ viên bi đỏ, $8$ viên bi vàng và $6$ viên bi xanh. Lấy ngẫu nhiên $4$ viên bi. Tính xác suất để các viên bi lấy được đủ cả $3$ màu.
Hướng dẫn giải:
Tổng số viên bi trong hộp là $24$
Gọi $\Omega$ là không gian mẫu.
Lấy ngẫu nhiên $4$ viên bi trong hộp, ta có ${C_{24}}^4$ cách lấy hay $n(\Omega)={C_{24}}^4=10626$
Gọi $A$ là biến cố lấy được các viên bi có đủ cả $3$ màu. Ta được các trường hợp sau:
| Viên bi đỏ | Viên bi vàng | Viên bi xanh | Cách chọn |
| $1$ | $1$ | $2$ | ${C_{10}}^1{C_8}^1{C_6}^2=1200$ |
| $1$ | $2$ | $1$ | ${C_{10}}^1{C_8}^2{C_6}^1=1680$ |
| $2$ | $1$ | $1$ | ${C_{10}}^2{C_8}^1{C_6}^1=2160$ |
Do đó, $n(A)=1200+1680+2160=5040$
Xác suất để các viên bi lấy được đủ cả $3$ màu là: $P(A)=\dfrac{n(A)}{n(\Omega)}=\dfrac{5040}{10626}\approx{}47,4\%$
Bài toán 2: Xếp ngẫu nhiên $10$ học sinh gồm $2$ học sinh lớp $12A$, $3$ học sinh lớp $12B$ và $5$ học sinh lớp $12C$ thành một hàng ngang. Xác suất để trong $10$ học sinh trên không có $2$ học sinh cùng lớp đứng cạnh nhau.
Hướng dẫn giải:
Cách 1: Ta xếp $5$ học sinh của lớp $12C$ thành một hàng ngang sao cho giữa các cặp học sinh lớp $C$ có đúng một chỗ trống thì sẽ có $2$ trường hợp. Vậy số cách xếp $10$ học sinh là: $5! \times 5! \times 2$
Cách 2: Ta xếp $5$ học sinh của lớp $12C$ thành một hàng ngang sao cho giữa một cặp học sinh lớp $C$ có đúng hai chỗ trống, còn lại giữa các cặp học sinh lớp $C$ khác có đúng một chỗ trống thì sẽ có $4$ trường hợp. Vậy số cách xếp $10$ học sinh là: $5! \times 2! \times 6 \times 3! \times 4$
Xác suất để trong $10$ học sinh trên không có $2$ học sinh cùng lớp đứng cạnh nhau là: $P=\dfrac{(5! \times 5! \times 2)+(5! \times 2! \times 6 \times 3! \times 4)}{10!}=\dfrac{11}{630}$
Bài toán 3: Gieo đồng thời hai cục xúc sắc cân đối, đồng chất. Tìm xác suất để số chấm ở mặt trên cục xúc sắc thứ nhất là $4$ và số chấm ở mặt trên cục xúc sắc thứ hai nằm trong khoảng $[3;5]$
Hướng dẫn giải:
Tổng số lần gieo ngẫu nhiên đồng thời hai cục xúc sắc cân đối, đồng chất là: $6 \times 6$
Ta có các trường hợp gieo thỏa yêu cầu bài toán như sau:
| Xúc sắc $1$ | $4$ | $4$ | $4$ |
| Xúc sắc $2$ | $3$ | $4$ | $5$ |
Xác suất để số chấm ở mặt trên cục xúc sắc thứ nhất là $4$ và số chấm ở mặt trên cục xúc sắc thứ hai nằm trong khoảng $[3;5]$ là: $P=\dfrac{3}{36}$
Bài toán 4: Chọn ngẫu nhiên $2$ học sinh từ một tổ có $9$ học sinh. Biết rằng xác suất chọn được $2$ học sinh nữ bằng $\dfrac{5}{18}$, hỏi tổ có bao nhiêu học sinh nữ?
Hướng dẫn giải:
Gọi số học sinh nữ là $n$ $(2\leq{}n>9, n\in{}\mathbb{N})$
Chọn ngẫu nhiên $2$ học sinh từ $9$ học sinh, ta có ${C_9}^2=36$ cách chọn.
Để chọn được $2$ học sinh nữ từ $n$ học sinh nữ, ta có ${C_n}^2 cách chọn.
Xác suất chọn được $2$ học sinh nữ là:
$P=\dfrac{{C_n}^2}{36}=\dfrac{5}{18}$
$\iff{}\dfrac{n(n+1)}{2 \times{36}}=\dfrac{5}{18}$
$\iff{}n=4$
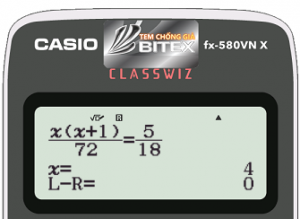
Vậy tổ có $4$ học sinh nữ.
About Toanbitexdtgd1
