BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI CÁC PHƯƠNG TRÌNH BẰNG CÁCH ĐƯA VỀ PHƯƠNG TRÌNH BẬC 2
- 25/01/2022
- 272 lượt xem
Phương trình chứa dấu căn thức
Phương trình $\sqrt{f\left( x \right)}=g\left( x \right)$ $\Leftrightarrow \left\{ \begin{align} & g\left( x \right)\ge 0 \\ & f\left( x \right)={{g}^{2}}\left( x \right) \\ \end{align} \right.$
Phương trình $\sqrt{f\left( x \right)}=\sqrt{g\left( x \right)}$ $\Leftrightarrow \left\{ \begin{align} & f\left( x \right)\ge 0\left( g\left( x \right)\ge 0 \right) \\ & f\left( x \right)=g\left( x \right) \\ \end{align} \right.$
Phương trình $\left( x+a \right)\left( x+b \right)\left( x+c \right)\left( x+d \right)=k$ với $a,b,c,d,k$ là những số cho trước, trong đó $a+b=c+d$
Ta có $\left( x+a \right)\left( x+b \right)\left( x+c \right)\left( x+d \right)=k$ $\Leftrightarrow \left[ {{x}^{2}}+(a+b)x+ab \right]\left[ {{x}^{2}}+(c+d)x+cd \right]=k$
Khi đó đặt $t=x^{2}+(a+b) x$, sau đó khai triển và sử dụng máy tính cầm tay để giải phương trình bậc 2 tìm nghiệm $t$ : $(t+a b)(t+c d)=k$
Từ đó tìm nghiệm $x$ bằng cách giải phương trình $x^{2}+(a+b) x-t=0$
Bên cạnh đó, khi gặp phải các bài toán giải phương trình tích, phương trình chứa mẫu số , phương trình trùng phương, chúng ta thường áp dụng phương pháp đưa về phương trình bậc 2 để giải quyết.
Một số bài toán thường gặp
Bài toán 1. Giải các phương trình sau:
a. $\sqrt{x}-x=2 \sqrt{x}+5$
b. $\dfrac{2 x+1}{x}+5 \dfrac{x}{2 x+1}=6$
Bình luận: $\sqrt{x}-x=2 \sqrt{x}+5$là một phương trình chứa căn. Để khử căn thức trong phương trình trên ta đặt $\sqrt{x}=t\left( t\ge 0 \right)$
Hướng dẫn giải
a. $\sqrt{x}-x=2 \sqrt{x}+5$
Đặt $t=\sqrt{x}\left( t\ge 0 \right)$
Khi đó phương trình đã cho trở thành $t-{{t}^{2}}=2t+5$ $\Leftrightarrow {{t}^{2}}+t+5=0$
Ta có: $\Delta=1-20<0$.
Suy ra phương trình đã cho vô nghiệm
b. $\dfrac{2 x+1}{x}+5 \dfrac{x}{2 x+1}=6$
Điều kiện $\left\{ \begin{align} & x\ne 0 \\ & x\ne \dfrac{-1}{2} \\\end{align} \right.$
Đặt $t=\dfrac{2x+1}{x}$. Khi đó phương trình đã cho trở thành
$t+\dfrac{5}{t}=6$ $\Leftrightarrow t^{2}+5=6 t \Leftrightarrow t^{2}-6 t+5=0 \Leftrightarrow(t-1)(t-5)=0 \Leftrightarrow \left[ \begin{array}{l}{t=1} \\ {t=5}\end{array}\right.$
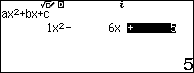
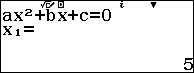
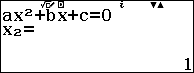
Với $t=1$ ta có $\dfrac{2 x+1}{x}=1 \Leftrightarrow x=2 x+1 \Leftrightarrow x=-1$
Với $t=5$ ta có $\dfrac{2 x+1}{x} =5\Leftrightarrow 5 x=2 x+1 \Leftrightarrow x=\dfrac{1}{3}$
Vậy phương trình đã cho có hai nghiệm $x=-1$ và $x=\dfrac{1}{3}$
Bài toán 2. (Phương trình chứa căn) Giải các phương trình sau:
a. $\sqrt{2{{x}^{2}}-3x-11}=\sqrt{{{x}^{2}}-1}$
b. $\sqrt{2{{x}^{2}}+3x-5}=x+1$
c. $\left( x-1 \right)\sqrt{{{x}^{2}}-3x}=0$
Hướng dẫn giải
a. $\sqrt{2{{x}^{2}}-3x-11}=\sqrt{{{x}^{2}}-1}$
$\Leftrightarrow \left\{ \begin{align} & 2{{x}^{2}}-3x-11\ge 0 \\ & {{x}^{2}}-1\ge 0 \\ & 2{{x}^{2}}-3x-11={{x}^{2}}-1 \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align} & x<\dfrac{3-\sqrt{97}}{4}\vee x>\dfrac{3+\sqrt{97}}{4} \\ & x<-1\vee x>1 \\ & {{x}^{2}}-3x-10=0 \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align} & x\le -1\vee x>\dfrac{3+\sqrt{97}}{4} \\& x=5\vee x=-2 \\\end{align} \right.$
$\Leftrightarrow \left[ \begin{align} & x=-2 \\ & x=5 \\\end{align} \right.$
Để giải nhanh và chính xác các phương trình và bất phương trình bậc 2 ta sẽ sử dụng máy tính cầm tay
Đối với Casio fx- 580VN X ta vào wz23 để giải các bất phương trình
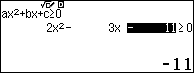
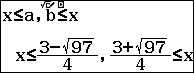
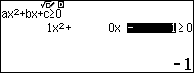
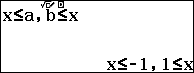
Để giải phương trình bậc 2 ta ấn w922
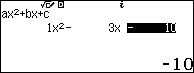
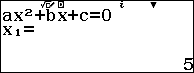
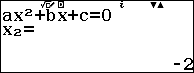
b. $\sqrt{2{{x}^{2}}+3x-5}=x+1$
$\Leftrightarrow \left\{ \begin{align} & x+1\ge 0 \\& 2{{x}^{2}}+3x+5={{\left( x+1 \right)}^{2}} \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align}& x\ge -1 \\ & 2{{x}^{2}}+3x+5={{x}^{2}}+2x+1 \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align} & x\ge -1 \\ & {{x}^{2}}+x+4=0 \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align} & x\ge -1 \\& \Delta =-15<0 \\\end{align} \right.$
Vậy phương trình đã cho vô nghiệm
Chú ý:
Đối với máy tính Casio fx-580VN X, dòng máy này có tính năng thông báo vô nghiệm khi giải phương trình, hệ phương trình
Để cài đặt tính năng thông báo vô nghiệm ta lần lượt bấm các phím sau qwR42
c. $\left( x-1 \right)\sqrt{{{x}^{2}}-3x}=0$
Trường hợp 1. $\left\{ \begin{align} & x-1=0 \\ & {{x}^{2}}-3x\ge 0 \\ \end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & x=1 \\ & x\le 0,x\ge 3 \\\end{align} \right.$ $\Leftrightarrow $ vô nghiệm
Trường hợp 2. ${{x}^{2}}-3x=0$ $\Leftrightarrow x\left( x-3 \right)=0$ $\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=3 \\ \end{align} \right.$
Vậy phương trình đã cho có hai nghiệm $x=0$ và $x=3$
Bài toán 3. Giải phương trình
a. $x(x+1)(x+2)(x+3)=1$
b. $x\left(x^{2}-4\right)(x+4)-1=0$
Hướng dẫn giải
a. $x(x+1)(x+2)(x+3)=1$
Ta có $0+3=1+2$ nên ta sẽ phân tích phương trình đã cho thành $\left( {{x}^{2}}+3x \right)\left( {{x}^{2}}+3x+2 \right)=1\left( * \right)$
Đặt $t={{x}^{2}}+3x$ . Khi đó phương trình (*) trở thành
$t\left( t+2 \right)=1$ $\Leftrightarrow {{t}^{2}}+2t-1=0$
${\Delta }’={{{b}’}^{2}}-ac=2>0$
Như vậy phương trình đã cho có 2 nghiệm phân biệt
${{t}_{1}}=-1+\sqrt{2}$; ${{t}_{2}}=-1-\sqrt{2}$
Với ${{t}_{1}}=-1+\sqrt{2}$ ta có ${{x}^{2}}+3x=-1+\sqrt{2}$ $\Leftrightarrow {{x}^{2}}+3x+1-\sqrt{2}=0$
$\Delta =9-4\left( 1-\sqrt{2} \right)=5+4\sqrt{2}>0$
Khi đó phương trình có hai nghiệm phân biệt ${{x}_{1}}=\dfrac{-3+\sqrt{5+4\sqrt{2}}}{2}$ ; ${{x}_{2}}=\dfrac{-3-\sqrt{5+4\sqrt{2}}}{2}$
Với ${{t}_{1}}=-1-\sqrt{2}$ ta có ${{x}^{2}}+3x=-1-\sqrt{2}$ $\Leftrightarrow {{x}^{2}}+3x+1+\sqrt{2}=0$
$\Delta =9-4\left( 1+\sqrt{2} \right)=5-4\sqrt{2}<0$. Suy ra phương trình vô nghiệm
Vậy phương trình đã cho có hai nghiệm phân biệt ${{x}_{1}}=\dfrac{-3+\sqrt{5+4\sqrt{2}}}{2}$ ; ${{x}_{2}}=\dfrac{-3-\sqrt{5+4\sqrt{2}}}{2}$
b. $x\left(x^{2}-4\right)(x+4)-1=0$
$x\left( {{x}^{2}}-4 \right)\left( x+4 \right)-1=0\Leftrightarrow x\left( x-2 \right)\left( x+2 \right)\left( x+4 \right)=1$
Ta có $0+2=-2+4$, do đó ta sẽ phân tích phương trình đã cho thành $\left( {{x}^{2}}+2x \right)\left( {{x}^{2}}+2x-8 \right)=1$ (*)
Đặt $t={{x}^{2}}+2x$. Khi đó phương trình (*) trở thành:
$t\left( t-8 \right)=1$ $\Leftrightarrow {{t}^{2}}-8t-1=0$$\Leftrightarrow \left[ \begin{align} & {{t}_{1}}=4+\sqrt{17} \\ & {{t}_{2}}=4-\sqrt{17} \\ \end{align} \right.$
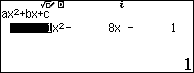
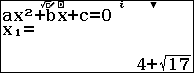
Với ${{t}_{1}}=4+\sqrt{17}$ ta được ${{x}^{2}}+2x=4+\sqrt{17}\Leftrightarrow {{x}^{2}}+2x-4-\sqrt{17}=0$ (1)
${\Delta }’={{{b}’}^{2}}-ac=1+4+\sqrt{17}=5+\sqrt{17}>0$
Như vậy phương trình (1) có hai nghiệm:
${{x}_{1}}=-1+\sqrt{5+\sqrt{17}}$ hoặc ${{x}_{2}}=-1-\sqrt{5+\sqrt{17}}$
Với ${{t}_{2}}=4-\sqrt{17}$ ta được ${{x}^{2}}+2x=4-\sqrt{17}\Leftrightarrow {{x}^{2}}+2x-4+\sqrt{17}=0$(2)
${\Delta }’={{{b}’}^{2}}-ac=1+4-\sqrt{17}=5-\sqrt{17}$
Như vậy phương trình (2) có hai nghiệm:
${{x}_{1}}=-1+\sqrt{5-\sqrt{17}}$hoặc ${{x}_{2}}=-1-\sqrt{5-\sqrt{17}}$
Vậy phương trình đã cho có bốn nghiệm phân biệt: ${{x}_{1}}=-1+\sqrt{5+\sqrt{17}}$,${{x}_{2}}=-1-\sqrt{5+\sqrt{17}}$ , ${{x}_{3}}=-1+\sqrt{5-\sqrt{17}}$ , ${{x}_{4}}=-1+\sqrt{5-\sqrt{17}}$
About Ngọc Hiền Bitex
