BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Củng cố các kỹ năng máy tính - giải bài thi THPT 2021 đợt 2 mã đề 102
- 18/08/2021
- 118 lượt xem
- 1. Xét ba vectơ
- 2. Thực hiện tích vectơ kép
- Ta chọn D.
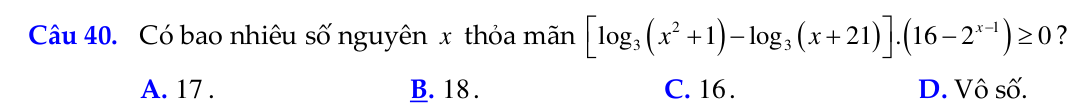
$$\left[\log_3(x^2+1)-\log_3(x+21)\right](16-2^{x-1}) \Leftrightarrow \left(\log_3(x^2+1)-\log_3(x+21)\right)(2^4-2^{x-1})\quad (1)$$
Điều kiện: $x>-21$
$$(1) \Leftrightarrow (x^2+1-x-21)(4-x+1)\geqslant 0 \Leftrightarrow x^3-6x^2-15x+100 \leqslant 0$$
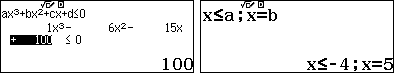
Kết hợp với điều kiện, $x$ nguyên và $-20\leqslant x\leqslant -4$ hay $x=5$. Có 18 số nguyên thoả ycbt. Ta chọn B.
Theo đề bài ta có $OA=OB=4, AB=4\sqrt2$ nên tam giác $ABC$ vuông cân tại $O$.
Do đó ta đặt $A(4\cos t; 4\sin t), B\left(4\cos \left(t+\dfrac{\pi}{2}\right);4\sin \left(t+\dfrac{\pi}{2}\right)\right)$. Như vậy $B(-4\sin t;4\cos t)$.
$P=CA+DB=\sqrt{(4\cos t-1)^2+(4\sin t -1)^2}+\sqrt{(-4\sin t-3)^2+(4\cos t-4)^2}$
Cài đặt máy tính CASIO fx-580VN X bảng chế độ một hàm và đon vị đo góc bằng radian.
- 1. Nhập hàm số như trên vào bảng trên máy tính
- 2. Chọn phạm vi $[0;2\pi]$. step $=2\pi/44$ ta có bảng như sau:
- 3. Với bước nhảy là 0,1 ta chấp nhận giá trị gần đúng của GTNN là 3,6 nên ta chọn D.
PS. Phương án C 
gây nhiễu, nhưng duyệt bảng trên máy tính, mọi giá trị của hàm số không nhỏ hơn 3,6.
Có thể chính xác hoá GTNN bằng cách xét trên đoạn $[0.57;0.71]$ bước nhảy 3 phần nghìn ta có:
$\approx \sqrt{13}$.
About TS. Nguyễn Thái Sơn
