Sử dụng số phức chứng minh tứ giác nội tiếp
- 16/08/2021
- 399 lượt xem
Bài viết sau đây dành cho học sinh đã tự học trong hè xong chương trình 12.
Bài viết cũng hướng đến đối tượng là các giáo viên trẻ. Cũng là một gợi ý về một sáng kiến kinh nghiệm nhằm bồi dưỡng học sinh giỏi.
Trong mặt phẳng cho 4 điểm $A, B, C, D$ phân biệt từng đôi một. Gọi $a, b, c, d$ lần lượt là các số phức nhận 4 điểm nói trên làm điểm biểu diễn.
Khi đó tứ giác $ABCD$ nội tiếp được khi và chỉ khi tỉ số kép $\dfrac{c-a}{c-b}:\dfrac{d-a}{d-b}$ là số thực.
Chứng minh
Ta có nhận xét: nếu $a$ và $c$ có điểm biểu diễn là $A$ và $C$ thì số phức $c-a$ có điểm biểu diễn là $M$ sao cho $\overrightarrow{OM}=\overrightarrow{OC}-\overrightarrow{OA}=\overrightarrow{AC}$.
Tương tự nếu $b$ và $c$ có điểm biểu diễn là $B$ và $C$ thì số phức $c-b$ có điểm biểu diễn là $N$ sao cho $\overrightarrow{ON}=\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BC}$.
Vậy $\arg \dfrac{c-a}{c-b}$ chính là góc $\widehat{ACB}$
Ghi nhớ: Muốn chia hai số phức dạng lượng giác ta lấy mô-đun chia cho mô-đun và lấy arg trừ cho arg.
Bây giờ ta chứng minh Mệnh đề 1:
$\dfrac{c-a}{c-b}:\dfrac{d-a}{d-b}$ là số thực khi và chỉ khi
$\arg\left(\dfrac{c-a}{c-b}:\dfrac{d-a}{d-b}\right)=0 \Leftrightarrow \arg \dfrac{c-a}{c-b}=\arg \dfrac{d-a}{d-b} \Leftrightarrow \widehat{ACB} =\widehat{ADB} \Leftrightarrow $ tứ giác $ABCD$ nội tiếp.
Cho ba số phức $a$, $b$ và $z$ sao cho $|a|=|b|=1$ lần lượt có điểm biểu diễn là $A, B, Z$. Gọi $W$ là điểm đối xứng của $Z$ qua đường thẳng $AB$. Khi đó $W$ là điểm biễu diễn của số phức $a+b-ab\overline{z}$.
Chứng minh
Xét hai số phức $\dfrac{z-a}{b-a}$ và $\dfrac{w-a}{b-a}$ ($w$ là số phức có điểm biểu diễn là $W$.)
VÌ $Z$ và $W$ đối xứng nhau qua đường thẳng $AB$ nên điểm biểu diễn của hai số phức nói trên đối xứng nhau qua trục hoành.
(điểm này bạn đọc tự tìm hiểu).
Khi đó số phức liên hợp của $\dfrac{z-a}{b-a}$ chính là $\dfrac{w-a}{b-a}$.
Vậy $\dfrac{w-a}{b-a}=\overline{\dfrac{z-a}{b-a}}=\dfrac{\overline{z}-\overline{a}}{\overline{b}-\overline{a}}=\dfrac{\overline{z}-\dfrac{1}{a}}{\dfrac{1}{b}-\dfrac{1}{a}}=\dfrac{ab\overline{z}-b}{a-b}\Rightarrow w=a+b-ab\overline{z}$. (đpcm)
Cho ba số phức $a$, $b$ và $c$ sao cho $|a|=|b|=|c|=1$ lần lượt có điểm biểu diễn là $A, B, C$. Gọi $H$ là trực tâm của tam giác $ABC$. Khi đó $H$ là điểm biễu diễn của số phức $a+b+c$.
Chứng minh
Giả sử $a=a_1+a_2i, b=b_1+b_2i, c=c_1+c_2i$. Các số $a_i, b_i, c_i (i=1,2)$ đều là số thực.
Gọi $K$ là điểm biểu diễn của số phức $a+b+c$. Khi đó toạ độ của vectơ $\overrightarrow{AK}$ bằng phần thực và phần ảo của số phức $(a+b+c)-a=b+c$, nghĩa là bằng $(b_1+c_1,b_2+c_2)$.
Ngoài ra $\overrightarrow{BC}=(c_1-b_1, c_2-b_2)$. Do đó $\overrightarrow{AH}.\overrightarrow{BC}=c_1^2+c_2^2-(b_1^2+b_2^2)=1-1=0 \Rightarrow AH \perp BC$. Tương tự $BH\perp AC$.
Gọi H là trực tâm tam giác ABC. Lấy một điểm D trên đường tròn ngoại tiếp tam giác ABC. Các đường thẳng kẻ từ B và C lần lượt song song với AD cắt đường tròn (ABC) tại các giao điểm thứ hai E và F. Gọi S, T, U lần lượt là điểm đối xứng của D, E, F qua BC, CA, AB. Chứng minh rằng tứ giác STHU nội tiếp.
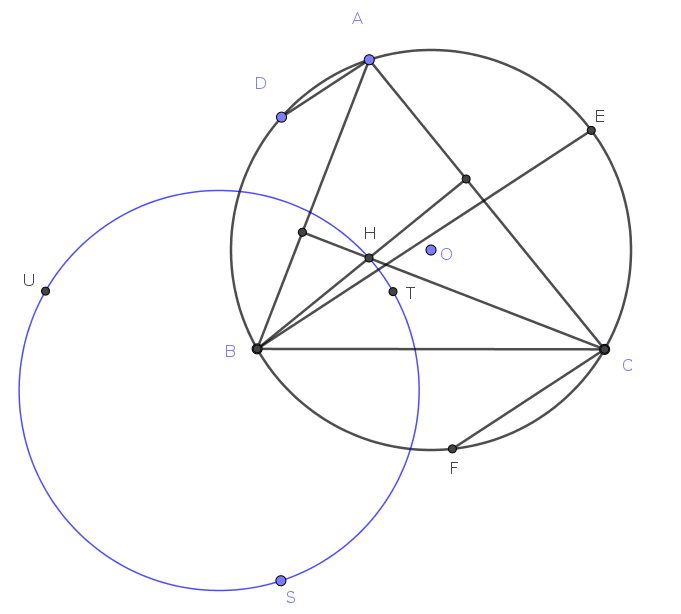
Giải
Ta có thể chọn đơn vị để đường tròn (ABC) là đường tròn đơn vị và không làm mất tính tổng quát ta giả sử $AD, BE, CF$ vuông góc với trục thực bằng cách quay một góc thích hợp.
Gọi $a, b, c$ là các số phức có mô-đun bằng 1 và nhận $A, B, C$ làm điểm biểu diễn, Khi đó trực tâm $H$ là điểm biểu diễn của số phức $a+b+c$. Vì $AD$ vuông góc với trục thực nên số phức $d-a$ là số thực, suy ra $d=\overline{a}$. Tương tự $e=\overline{b}, f=\overline{c}$.
Do tính chất đối xứng qua trục nên theo mệnh đề 2, ta có: $s = b + c − bc\overline{d} = b + c − abc$.
Tương tự $t = c + a − ca\overline{e} = c + a − abc$, $u = a + b − ab\overline{f} = a + b − abc$.
Ta tính $w=\dfrac{s-t}{s-u}:\dfrac{h-t}{h-u}=\dfrac{b-a}{c-a}:\dfrac{b+abc}{c+abc}=\dfrac{b-a}{c-a}\times \dfrac{c+abc}{b+abc}=\dfrac{b-a}{c-a}\times \dfrac{c(1+ab)}{b(1+ac)}$.
Do đó $\overline{w}=\dfrac{\dfrac{1}{b}-\dfrac{1}{a}}{\dfrac{1}{c}-\dfrac{1}{a}}\times \dfrac{\dfrac{1}{c}+\dfrac{1}{abc}}{\dfrac{1}{b}+\dfrac{1}{abc}}=\dfrac{b-a}{c-a}\times \dfrac{c(1+ab)}{b(1+ac)}$.
Vậy $\overline{w}=w$ nên $w$ là số thực. Suy ra tứ giác $STHU$ nội tiếp.
Một bài tập gợi ý:
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay