Sử dụng số phức giải toán hình học phẳng

1. Nêu bài toán

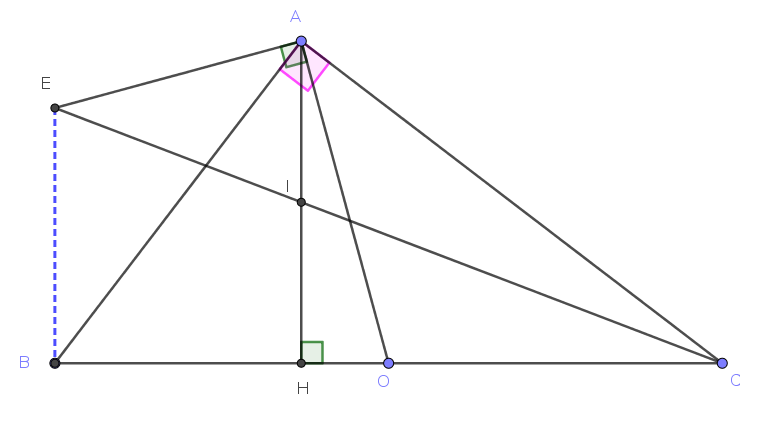
Chúng tôi không cho rằng bài toán này là dễ. Vì vậy chúng tôi gợi ý phương pháp dùng số phức.
PS. Loạt bài về việc sử dụng số phức để giải các bài toán Hình học phẳng là một gợi ý cho các GV trẻ thực hiện các dự án nghiên cứu của mình nhằm bồi dưỡng học sinh giỏi. Các giáo viên trung học ở Đài Loan họ sử dụng nội dung này để bồi dưỡng học sinh dự thi IMO.

2. Các kiến thức chuẩn bị.

Chứng minh.

Trong bài Sử dụng số phức chứng minh tứ giác nội tiếp chúng tôi đã chứng minh điểm $U$ đối xứng của $Z$ qua $BC$ là điểm biểu diễn của số phức $u=b+c-bc\overline{z}$

Khi đó $H$ là trung điểm của $ZU$ nên $H$ là điểm biểu diễn của số phức $\dfrac{z+u}{2}=\dfrac{z+b+c-bc\overline{z}}{2}$.

Chứng minh.

Gọi $H$ là trung điểm của $BC$. Khi đó $H$ là điểm biểu diễn của số phức $h=\dfrac{b+c}{2}$. Chứng minh $O, H, T$ thẳng hàng và $OH.OT=1$ nghĩa là $TA\perp OA$ và t $TB\perp OB$.

Xét số phức $\dfrac{h}{t}=\dfrac{b+c}{2}\times \dfrac{\overline{b}+\overline{c}}{2}=\dfrac{b\overline{b}+c\overline{c}+(b\overline{c}+c\overline{b})}{4}=\dfrac{2+(b\overline{c}+c\overline{b})}{4}$. Ta thấy $b\overline{c}+c\overline{b}$ là số thực (vì nó bằng liên hợp của nó). Do đó $\dfrac{h}{t}$ là số thực, nghĩa là $\arg\dfrac{h}{t}=0 \Rightarrow \widehat{\overrightarrow{OT},\overrightarrow{OH}}=0$. Vậy ba điểm $O, T, H$ thẳng hàng.
$OH.OT=|h||t|=\left|\dfrac{b+c}{2}\times \dfrac{2bc}{b+c}\right|=|bc|=|b||c|=1$. (đpcm)

Chứng minh.
Để tránh bị rối, tạm thời chúng tôi chưa chứng minh mệnh đề này. Ta chấp nhận để giải toán.

Bây giờ chúng ta giải bài toán đã nêu:

Chọn đơn vị thích hợp ta được đường tròn ngoại tiếp tam giác $ABC$ là đường tròn đơn vị nhận tâm $O$ làm gốc toạ độ và không làm mất tính tổng quát ta chọn $BC$ nằm trên trục hoành.

Khi đó $b$ và $c$ là số thực có giá trị tuyệt đối bằng 1. Nói cách khác $b=-1, c=1$.

Điểm $H$ là điểm biểu diễn của số phức $h=\dfrac12(a+b+c-bc\overline{a})=\dfrac{a+\overline{a}}{2}=\dfrac{a^2+1}{2a}$. Ta thấy $\overline{h}=h$.
(lưu ý $a$ là số phức có mô-đun bằng 1.)

Vì $I$ là trung điểm $AH$ nên $I$ là điểm biểu diễn của số phức $\dfrac{a+h}{2}=\dfrac{3a+\overline{a}}{4}=\dfrac{3a^2+1}{4a}$.

Gọi $E’$ là giao điểm của tiếp tuyến tại $A$ và tiếp tuyến tại $B$. Khi đó $E’$ là điểm biểu diễn của số phức $z=\dfrac{2}{\overline{a}+\overline{b}}=\dfrac{2}{\overline{a}-1}=\dfrac{2a}{1-a}$ (mệnh đề 2). Suy ra $\overline{z}=\dfrac{2}{a-1}$

Gọi $I’$ là giao điểm của $CE’$ và $AH$. Theo mệnh đề 3, $I’$ là điểm biểu diễn của số phức $$j=\dfrac{(\overline{c}z-c\overline{z})(a-h)-(c-z)(\overline{a}h-a\overline{h})}{(\overline{c}-\overline{z})(a-h)-(c-z)(\overline{a}-\overline{h})}=
\dfrac{(z-\overline{z})(a-h)-(1-z)(\overline{a}h-ah)}{(1-\overline{z})(a-h)-(1-z)(\overline{a}-h)}$$

Ta tính được $\overline{a}-h=-(a-h)$ và $\overline{a}-a=-2(a-h)$ nên ta thu gọn được:
$$j=\dfrac{z-\overline{z}+2h(1-z)}{2-(z+\overline{z})}$$

Ta tính thêm $z+\overline{z}=-2, z-\overline{z}=\dfrac{-2(a+1)}{a-1}, 1-z=\dfrac{3a-1}{a-1}$.

Khi đó $$j=\dfrac{-2a(a+1)+(a^2+1)(3a-1)}{4a(a-1)}=\dfrac{3a^2+1}{4a}$$

Suy ra $I’\equiv I \Rightarrow E’=E$. Do đó $EB$ là tiếp tuyến tại $B$, suy ra đpcm.

Bài toán tương tự dành cho bạn đọc.

Hướng dẫn: Để chứng minh $IQ\perp IM$ ta chứng minh số phức $\dfrac{m-j}{q-j}$ là số thuần ảo.

Ở đây ký hiệu $j$ số phức có điểm biểu diễn là $I$ nhằm tránh nhầm lẫn với số đơn vị ảo.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.