Dùng Máy tính Casio fx-880BTG khai căn một biểu thức chứa căn

Từ (2) suy ra $y=\dfrac{\sqrt{B}}{2x}$ thay vào (1): $x^2+\dfrac{B}{4x^2}=A\Leftrightarrow x^4-Ax^2+\left(\dfrac{\sqrt{B}}{2}\right)^2=0 $.

Vậy $x^2$ và $y^2$ là hai nghiệm $x_1, x_2$ của phương trình bậc hai

ta quy ước nghiệm lớn $x_1$ là $x^2$ và do đó $x_2$ là $y^2$.

Vậy

 
Tính $\sqrt{49+20\sqrt6}-\sqrt{33-12\sqrt6}$
 

 
Ta có: $\sqrt{49+20\sqrt6}=\sqrt{25+24+20\sqrt6}=\sqrt{(5+\sqrt{24})^2}=5+\sqrt{24}$
 

Bấm hai lần nhập lại số

 
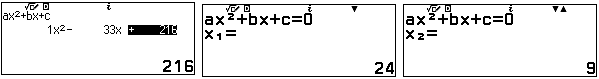
Ta có: $\sqrt{33-12\sqrt6}=\sqrt{24+9-12\sqrt6}=\sqrt{(\sqrt{24}-3)^2}=\sqrt{24}-3$

 
Vậy $\sqrt{49+20\sqrt6}-\sqrt{33-12\sqrt6}=5+\sqrt{24}-(\sqrt{24}-3)=8$

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.