BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG MÁY TÍNH CASIO FX-880BTG GIẢI BÀI TOÁN TÌM GTLN, GTNN
- 12/09/2022
- 13,182 lượt xem
Câu 1: Tìm GTLN của hàm số $y=\dfrac{2x^2+3x+3}{x+1}$ trên đoạn $[0;2]$.
A. $3$. B. $\dfrac{17}{3}$. C.$6$. D. $5$.
Lời giải
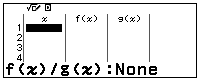
Bước 1: Chọn phương thức tính toán Bảng giá trị.
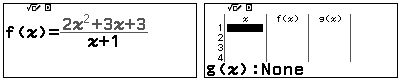
Bước 2: Nhập hàm số $f(x)=\dfrac{2x^2+3x+3}{x+1}$.
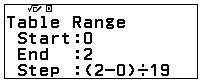
Bước 3: Nhập $Start=0$, $End=2$, $Step=(2-0):44$.
Bước 4: Quan sát bảng giá trị $f(x)$ đưa ra kết luận.
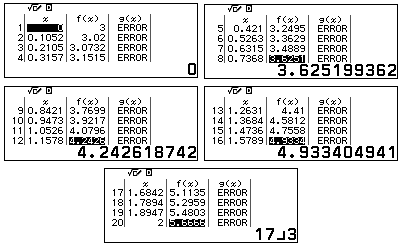
Vậy giá trị lớn nhất của hàm số là $\dfrac{17}{3}$.
Chọn B.
Bài 2: Tìm giá trị lớn nhất của hàm số $y=\sqrt{3-2x-x^2}$ là
A. $1$. B. $2$. C.$3$. D. $4$.
Lời giải
Bước 1: Điều kiện của $f(x)$ $\Rightarrow 3-2x-x^2$ ≥ $0$ $\Leftrightarrow -3$≤$x$≤$1$.
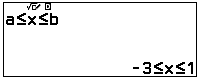
Bước 2: Chọn phương thức tính toán bảng tính.
Bước 3: Nhập hàm số $f(x)=\sqrt{3-2x-x^2}$.
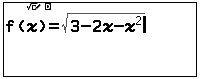
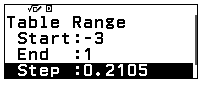
Bước 4: Nhập $Start=-3$, $End=1$, $Step=(1-(-3)):44$.
Bước 5: Quan sát bảng giá trị $f(x)$ đưa ra kết luận.
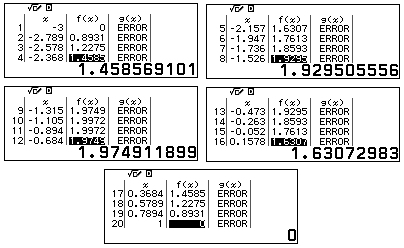
Vậy giá trị lớn nhất của hàm số là $2$.
Chọn B.
Chia sẻ
About Toanbitexdtgd1
