BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Số hạng tổng quát của dãy số quy nạp
- 12/11/2021
- 560 lượt xem
Nhiều năm trước đây, nhiều giáo viên đã có những nghiên cứu thú vị về việc xây dựng một dãy số quy nạp trong đó mỗi số hạng dựa vào hai số hạng đứng ngay trước nó cộng thêm một biểu thức, ví dụ nghiên cứu của Thầy Nguyễn Tất Thu (THPT BC Lê Hồng phong, Đồng Nai) đăng trên toanmath.com. Tham khảo nghiên cứu đó và dựa vào một đề thi HSG MTCT cấp THCS của Bộ Giáo dục và Đào tạo năm 2007, chúng tôi cụ thể hóa bài toán của Bộ và đáp số của nó như sau:
Đề thi năm 2007- câu 5: Cho dãy số $(u_n)$ xác đinh bởi: $$\left\lbrace\begin{array}{l}u_0=-2007; u_1=-2006\\ u_{n+2}=u_{n+1}+u_n+2007\end{array}\right.$$
|
Để trả lời câu 1, ngày nay chúng ta sẽ xử lý trên MTCT Casio fx-580VN X như sau:
MTCT tự động lưu vào Ans sau đó được đẩy vào PreAns
MTCT tự động lưu vào Ans.
Viết lên màn hình nhấn (enter) ta được $u_2$ 
, sau đó nhân (enter) đủ 47 lần ta được $u_{49}$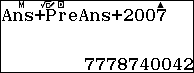 
Để trả lời câu 2 phù hợp với trình độ THCS, chúng tôi giới thiệu kết quả sau cho HS và sẽ chứng minh kết qủa đó cho GV.
| Cho dãy số $(u_n)$ xác đinh bởi: $$\left\lbrace\begin{array}{l}u_0=\alpha; u_1=\beta\\ u_{n+2}+au_{n+1}+bu_n= c\end{array}\right.$$ trong đó $a,b,c \in \mathbb{R}$. Số hạng tổng quát của dãy số nói trên có dạng $$u_n=Ax_1^n+Bx_2^n+C$$ trong đó $A, B, C$ là ba số mà ta sẽ xác định, $x_1,x_2$ là hai nghiệm phân biệt của phương trình: $x^2+ax+b=0$. |
Trở lại bài toán, giải phương trình bậc hai lần lượt lưu $x_1, x_2$ vào $A$ và $B$.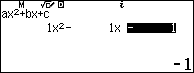
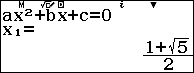
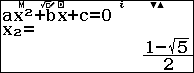
Để tìm các hệ số của $x_1^n, x_2^n$ và hệ số tự do, ta giải hệ ba phương trình (bằng cách cho $n=0,1,2$ vào hệ thức quy nạp):
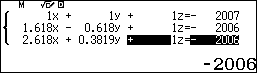
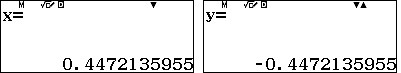
Vậy $$u_n=\dfrac{\sqrt5}{5}\left(\dfrac{1+\sqrt5}{2}\right)^n-\dfrac{\sqrt5}{5}\left(\dfrac{1-\sqrt5}{2}\right)^n-2007$$
About TS. Nguyễn Thái Sơn
