BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG CASIO FX 580VNX ĐỂ TÌM CÁC HỆ SỐ CỦA PHƯƠNG TRÌNH LOGARIT
- 14/11/2021
- 509 lượt xem
Đề bài
Cho phương trình ${{\log }_{5}}\left( \dfrac{2\sqrt{x}+1}{x} \right)=2{{\log }_{3}}\left( \dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}} \right)$, biết rằng phương trình đã cho có một nghiệm duy nhất có dạng $x=a+b\sqrt{c}$$a,b,c\in \mathbb{Z}$. Tính $S={{a}^{2}}+{{b}^{2}}-{{c}^{2}}$
A. $S={{a}^{2}}+{{b}^{2}}-{{c}^{2}}=5$
B. $S={{a}^{2}}+{{b}^{2}}-{{c}^{2}}=8$
C. $S={{a}^{2}}+{{b}^{2}}-{{c}^{2}}=9$
D. $S={{a}^{2}}+{{b}^{2}}-{{c}^{2}}=11$
Hướng dẫn giải
Sử dụng lệnh SOLVE qr để tìm nghiệm của phương trình và lưu vào ô nhớ A
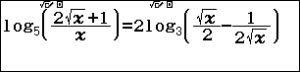
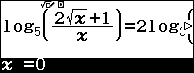
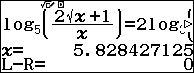
Vì kết quả cho nghiệm là một số thập phân nên nghiệm sẽ có chứa căn thức do đó đoán $c\ge 2$
Như vậy ta sẽ thử $c=2$ và sau đó thử dần lên các số nguyên tố khác.
Vậy $x=a+b\sqrt{2}\Leftrightarrow A=a+b\sqrt{2}$
Dùng phương thức TABLE w8 để dò nghiệm
Ta có $A=a+b\sqrt{2}\Rightarrow a=f\left( x \right)=A-b\sqrt{2}=A-x\sqrt{2}$
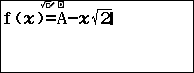
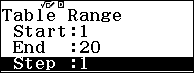
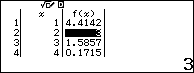
Dựa vào kết quả ta nhận $x=2,f\left( x \right)=3$ suy ra $a=f\left( x \right)=3,b=x=2$
Vậy ${{a}^{2}}+{{b}^{2}}-{{c}^{2}}={{3}^{2}}+{{2}^{2}}-{{2}^{2}}=9$
Mọi ý kiến đóng góp và các câu hỏi thắc mắc về các bài viết hướng dẫn giải toán casio cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
