BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
DÃY SỐ QUY NẠP
- 10/11/2021
- 1,885 lượt xem
Dựa vào hai biến nhớ 
và 
ta có thể xây dựng một dãy số qui nạp dựa vào hai số đứng liềm trước.
Tuy nhiên trong các đề thi gần đây để kiểm tra trình độ học sinh, bài thi thường yêu cầu xây dựng một dãy số $(u_n)$ dựa vào hai số đứng liền trước và chỉ số $n$.
Giả sử dãy số $(u_n)$ được xác định như sau:
- $u_1=a$
- $u_2=b$
- $u_n=p u_{n-1}+q u_{n-2} + f(n)$ với $n\geqslant 3$
Tính $u_m$.
Thuật toán xây dựng dãy số này như sau:
$$x=x+1:A=pB+qA+f(x):x=x+1:B=pA+qB+f(x)$$
Bấm CALC máy tính hỏi $x$ ta nhập $2$, máy tính hỏi $A$ ta nhập $a$, máy tính hỏi $B$ ta nhập $b$. Sau đó nhấn dấu 
cho đến khi chỉ số $x$ đứng tại $m$, nhấn lần nữa ta sẽ được giá trị của $u_m$.
Ví dụ: Cho dãy số $(u_n)$ xác định bởi $u_1=1, u_2=3$ và $$u_n=2u_{n-1}-3u_{n-2}+n^2\quad n \geqslant 3$$
Tính $u_{39}, u_{40},u_{41}$.
- Viết lên màn hình
- Bấm
máy hỏi $x$ ta nhập 
, máy hỏi $B$ ta nhập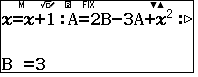 
, máy hỏi $A$ ta nhập 
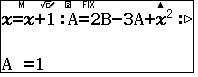. - Nhấn dấu liên tục cho đến khi
nhấn ta có $u_{39} = $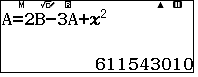 
- Nhấn
- Nhấn
Riêng $u_{41}$ ta cần viết ra giá trị đúng của nó:
Nhập $u_{39}$ vào máy tính 
Nhập $u_{40}$ vào máy tính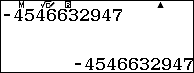 
Tính $u_{41}$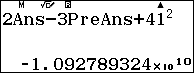 
Xử lý số tràn màn hình 
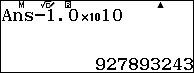
Vậy $u_{41}=-10927893243$
About TS. Nguyễn Thái Sơn
