BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải tiếp bài toán của Thầy Đang Nguyễn
- 13/03/2020
- 1,633 lượt xem
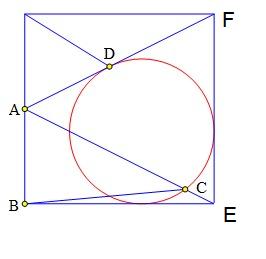
Gọi thêm hai đỉnh hình vuông là $E$ và $F$ như hình vẽ.
Ta có $\widehat{DAC}=\widehat{FAE}=2\arctan\dfrac12$
Phương trình đường thẳng $AF$ là $x-2y+1=0$ do đó toạ độ điểm $D$ (hình chiếu vuông góc của tâm $I$ trên $AF$) là $D\left(\dfrac{\sqrt5}{5};\dfrac{5+\sqrt5}{10}\right)$.
Ngoài ra theo tính toán ở trên ta có $C\left(\dfrac{\sqrt5+2}{5};\dfrac{3-\sqrt5}{10}\right)$.
Suy ra $CD^2=\dfrac{10+2\sqrt5}{25}$.
Nhận xét rằng $BD=BC$ do đó: $$\cos \widehat{CBD}=\dfrac{2BC^2-DC^2}{2BC^2}=\dfrac35$$
Cuối cùng vì $\arccos\dfrac35=2\arctan\dfrac12$
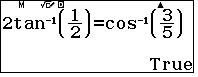
nên $\widehat{DAC}=\widehat{DBC}$ là điều cần chứng minh.
PS. Cám ơn gợi ý của thầy Vac Nguyễn.
Các tính toán phức tạp về các số vô tỉ được thực hiện trên máy tính Casio fx-580 VNX
Vì $AE=AF$ nên có thể tính góc $\widehat{FAE}$ cách khác như sau: $$\cos\widehat{FAE}=\dfrac{2AF^2-EF^2}{2AF^2}=\dfrac{3}{5}$$
About TS. Nguyễn Thái Sơn
