BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI CÁC CÂU NHẬN BIẾT THÔNG HIỂU TRONG ĐỀ THI THỬ NGÀY 10/07/2020
- 20/07/2020
- 115 lượt xem
Nhằm giúp các bạn ôn luyện tốt hơn, thay vì chỉ đăng đáp án như trước thì đợt này Diễn đàn sẽ thực hiện giải một số câu trong đề thi trên máy tính Casio fx-580VN X. Hị vọng nó sẽ giúp ích được các bạn trong kì thi tuyển sinh THPT QG 2020 sắp tới. Trong bài viết này Diễn đàn sẽ thực hiện giải trước 25 câu đầu của đề thi.
LINK: http://bitexedu.com/de-thi-thu-ngay-10-07-2020/
Câu 1. Có bao nhiêu số tự nhiên gồm ba chữ số phân biệt được lập từ các chữ số khác 0?
| A. ${C}_9^3$. | B. $A_{10}^3$. |
| C. ${9^3}$. | D. $A_9^3$. |
Lời giải
Mỗi số được viết tương ứng với một chỉnh hợp chập 3 của 9 là $A_9^3$. Chọn D.
Câu 2. Cho cấp số nhân $\left( {{u_n}} \right)$ với ${u_1} = 2$ và ${u_4} = 250$. Công bội của cấp số nhân đã cho bằng
| A. $125$. | B. $5$. |
| C. $\dfrac{1}{5}$. | D. $\dfrac{{125}}{3}$. |
Lời giải
${u_4} = {u_1}.{q^3} \Rightarrow {q^3} = \dfrac{{{u_4}}}{{{u_1}}} = 125 \Leftrightarrow q = 5$. Chọn B.
Câu 3. Nghiệm của phương trình ${\log _2}\left( {3{\text{x}} – 2} \right) = 3$ là
| A. $x = 8$. | B. $x = \dfrac{{10}}{3}$. |
| C. $x = 1$. | D. $x = \dfrac{1}{3}$. |
Lời giải
Chọn B
Cách 1. ${\log _2}\left( {3{\text{x}} – 2} \right) = 3 \Leftrightarrow 3{\text{x}} – 2 = {2^3} \Leftrightarrow x = \dfrac{{10}}{3}$.
Cách 2. Sử dụng tính năng Calc trên máy tính để thử đáp án với $f\left( x \right) = {\log _2}\left( {3x – 2} \right) – 3$
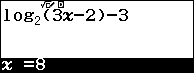
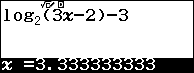
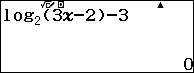
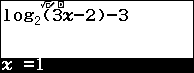
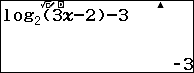
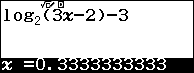
Như vậy, chỉ có đáp án B thỏa yêu cầu đề bài.
Câu 4. Tính thể tích của khối tứ diện $ABCD$, biết $AB,AC,AD$ đôi một vuông góc và lần lượt có độ dài bằng $2,4,3$?
| A. $24$. | B. $8$. |
| C. $4$. | D. $3$. |
Lời giải
${V_{ABC{\text{D}}}} = \dfrac{1}{3}AB.{S_{ACD}} = \dfrac{1}{6}AB.AC.AD = 4$.
Chọn C.
Câu 5. Tập xác định của hàm số $y = {\log _3}\left( {x – 2} \right)$ là
| A. $\left[ {2; + \infty } \right)$ | B. $\left( { – \infty ; + \infty } \right)$. |
| C. $\left( {2; + \infty } \right)$. | D. $\left[ { – 2; + \infty } \right)$. |
Lời giải
Chọn C.
Câu 6. Tìm họ nguyên hàm của hàm số $f(x) = \sin(2020ax+1)$ (Với $a$ là tham số khác $0$)
A. $\int {\sin (2020ax + 1)dx = \dfrac{1}{{2020}}\cos 2020x + C} $.
B. $\int {\sin (2020ax + 1)dx = \cos 2020ax + C} $.
C. $\int {\sin (2020ax + 1)dx = – \dfrac{1}{{2020a}}\cos (2020ax + 1) + C}$.
D. $\int {\sin (2020ax + 1)dx} = \cos 2020x + C$.
Lời giải
\[\begin{aligned} \int{\sin (2020ax+1)dx}&=\frac{1}{2020a}\int{\sin (2020ax+1)d(2020ax+1)} \\ & =-\frac{1}{2020a}\cos (2020ax+1)+C \end{aligned}\]
Chọn C.
Câu 7. Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB =2a, AD = a$ cạnh bên $SA$ vuông góc với đáy, $SA=3a$.Thể tích của khối chóp $S.ABCD$ là
| A. $V = \dfrac{3}{2}{a^3}$. | B. $V = 3{a^3}$. |
| C. $V = 2{a^3}$. | D. $V = 9{a^3}$. |
Lời giải
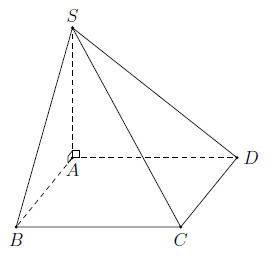
$V = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}3a.a.2a = 2{a^3}$. Chọn C.
Câu 8. Cho khối nón có chiều cao $h= 2$ và bán kính đáy $r= 3$. Thể tích của khối nón đã cho là
| A. $24\pi $. | B. $6\pi $. |
| C. $4\pi $. | D. $36\pi $. |
Lời giải
Chọn B.
Câu 9. Cho khối cầu có bán kính $R = 2$. Thể tích của khối cầu đã cho là
| A. $\dfrac{{32\pi }}{3}$. | B. $256\pi $. |
| C. $64\pi $. | D. $16\pi $. |
Lời giải
Chọn A.
Câu 10. Cho hàm số $y = a{x^3} + b{x^2} + cx + d$. Hỏi hàm số luôn đồng biến trên$\mathbb{R}$ khi nào?
A. $\left[ \begin{gathered} a = b = 0,c > 0 \hfill \\ a > 0;{b^2} – 3ac \leqslant 0 \hfill \\\end{gathered} \right.$.
B. $\left[ \begin{gathered} a = b = 0,c > 0 \hfill \\ a > 0;{b^2} – 3ac \geqslant 0 \hfill \\\end{gathered} \right.$.
C. $\left[ \begin{gathered} a = b = 0,c > 0 \hfill \\ a < 0;{b^2} – 3ac \leqslant 0 \hfill \\\end{gathered} \right.$.
D. $\left[ \begin{gathered} a = b = c = 0 \hfill \\ a < 0;{b^2} – 3ac < 0 \hfill \\\end{gathered} \right.$.
Lời giải
Hàm số đồng biến khi $y’ \geqslant 0\forall x \in \mathbb{R}$, do đó ta có:
$y’ = 3a{x^2} + 2bx + c \geqslant 0,\forall x \in \mathbb{R} \Leftrightarrow \left[ \begin{gathered} a = b = 0,c > 0 \hfill \\a > 0;{b^2} – 3ac \leqslant 0 \hfill \\ \end{gathered} \right.$.
Chọn A.
Câu 11. Cho $a$ là số thực dương tùy ý, $\ln \dfrac{{\text{e}}}{{{a^2}}}$ bằng
| A. $2\left( {1 + \ln a} \right)$. | B. $1 – \dfrac{1}{2}\ln a$. |
| C. $2\left( {1 – \ln a} \right)$. | D. $1 – 2\ln a$. |
Lời giải
Chọn D.
Câu 12. Cho hình nón có bán kính đáy $r = \sqrt 3$ và độ dài đường sinh $l = 4$. Tính diện tích xung quanh ${S_{xq}}$ của hình nón đã cho.
| A. ${S_{xq}} = 12\pi $. | B. ${S_{xq}} = 4\sqrt 3 \pi $. |
| C. ${S_{xq}} = \sqrt {39} \pi $. | D. ${S_{xq}} = 8\sqrt 3 \pi $. |
Lời giải
Ta có ${S_{xq}} = \pi Rl$. Nên ${S_{xq}} = \pi \sqrt 3 .4 = 4\sqrt 3 \pi $. Chọn B.
Câu 13. Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên đoạn $\left[ { – 4\,;\,0} \right]$ và có đồ thị là đường cong trong hình vẽ bên. Hàm số $f\left( x \right)$ đạt cực tiểu tại điểm nào dưới đây?
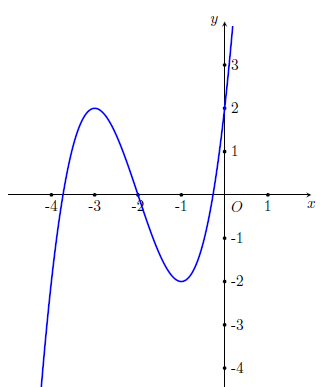
| A. $x = – 1$. | B. $x = – 3$. |
| C. $x = 2$. | D. $x = – 2$. |
Lời giải
Chọn A.
Câu 14. Đồ thị hàm bậc bốn trùng phương nào dưới đây có dạng đồ thị hình vẽ bên
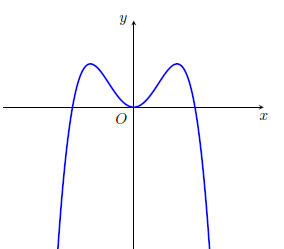
| A. $f\left( x \right) = {x^4} – 2{x^2}$. | B. $f\left( x \right) = – {x^4} + 2{x^2}$. |
| C. $f\left( x \right) = {x^4} + 2{x^2}$. | D. $f\left( x \right) = – {x^4} + 2{x^2} – 1$. |
Lời giải
Đường cong trong hình vẽ là đồ thị hàm số trùng phương $f\left( x \right) = a{x^4} + b{x^2} + c$ (với $a \ne 0$).
Từ đồ thị hàm số ta thấy
– Đồ thị hàm số có hướng đi xuống nên $a < 0$.
– Đồ thị hàm số có $3$ cực trị nên $ab < 0$.
– Đồ thị hàm số đi qua gốc tọa độ nên $c = 0$.
Dựa vào $4$ đáp án thì chỉ có hàm số $f\left( x \right) = – {x^4} + 2{x^2}$ thỏa mãn. Chọn B.
Câu 15. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số $y = 10 + \dfrac{1}{{x – 10}}$?
| A. $y = 0$. | B. $x = 0$. |
| C.$y = 10$. | D. $x = 10$. |
Lời giải
Ta có $\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \left( {10 + \dfrac{1}{{x – 10}}} \right) = 10$$ \Rightarrow y = 10$ là đường tiệm cận ngang của đồ thị hàm số. Chọn C.
Câu 16. Tập nghiệm của bất phương trình ${\left( {\dfrac{2}{3}} \right)^{4x}} \leqslant {\left( {\dfrac{3}{2}} \right)^{2 – x}}$ là:
| A. $\left( { – \infty ;\, – \dfrac{2}{3}} \right]$. | B. $\left[ { – \dfrac{2}{3};\, + \infty } \right)$. |
| C. $\left( { – \infty ;\,\dfrac{2}{5}} \right]$. | D. $\left( {\dfrac{2}{3};\, + \infty } \right)$. |
Lời giải
Chọn B
Cách 1: Ta có: ${\left( {\dfrac{2}{3}} \right)^{4x}} \leqslant {\left( {\dfrac{3}{2}} \right)^{2 – x}} \Leftrightarrow {\left( {\dfrac{3}{2}} \right)^{ – 4x}} \leqslant {\left( {\dfrac{3}{2}} \right)^{2 – x}} \Leftrightarrow – 4x \leqslant 2 – x \Leftrightarrow x \geqslant – \dfrac{2}{3}$.
Cách 2: Sử dụng Calc trên máy tính để thử đáp án.
Ta nhập hàm số $f\left( x \right) = {\left( {\dfrac{2}{3}} \right)^{4x}} – {\left( {\dfrac{3}{2}} \right)^{2 – x}}$
Sau đó sử dụng Calc với giá trị $x = – \dfrac{2}{3}$
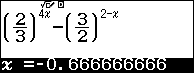
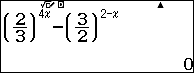
Nhận, vậy ta loại đáp án D.
Tiếp tục sử dụng Calc với giá trị $x = – 0.7$
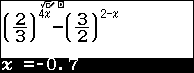
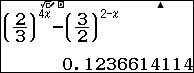
Loại, vậy ta loại được đáp án A và C. Ta chọn B.
Lời bình: Trong những bài toán có thể sử dụng máy tính để kiểm tra đáp án như dạng bài tìm tập nghiệm hay tập xác định của hàm số thì ta nên sử dụng máy tính nhằm tiết kiệm thời gian và đầu óc để thực hiện những bài khó hơn.
Câu 17. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:
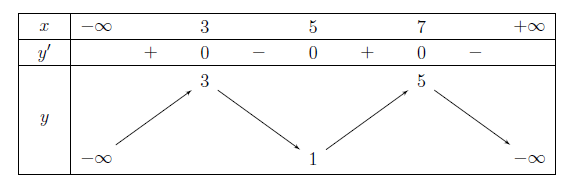
Phương trình $f\left( x \right) = 4$ có bao nhiêu nghiệm thực?
| A. $4$. | B. $2$. | C. $3$. | D. $0$. |
Lời giải
Số nghiệm của phương trình $f\left( x \right) = 4$ bằng số giao điểm của đường thẳng $y = 4$ và đồ thị hàm số $y = f\left( x \right)$.
Từ bảng biến thiên ta thầy đường thẳng $y = 4$ cắt đồ thị hàm số $y = f\left( x \right)$ tại $2$ điểm phân biệt. Vậy phương trình $f\left( x \right) = 4$ có 4 nghiệm. Chọn B.
Câu 18. Cho $\int\limits_0^1 {f\left( x \right){\text{d}}x} = – 2$ và $\int\limits_0^1 {g\left( x \right){\text{d}}x} = 7$, khi đó $\int\limits_0^1 {\left[ {2f\left( x \right) – 3g\left( x \right)} \right]{\text{d}}x} $bằng
| A. $ – 12$. | B. $25$. |
| C. $ – 25$. | D. $17$. |
Lời giải
Ta có: $\int\limits_0^1 {\left[ {2f\left( x \right) – 3g\left( x \right)} \right]{\text{d}}x} = 2\int\limits_0^1 {f\left( x \right){\text{d}}x} – 3\int\limits_0^1 {g\left( x \right){\text{d}}x} = 2.\left( { – 2} \right) – 3.7 = – 25$. Chọn C.
Câu 19. Mô đun của số phức $z = 3 + 4i$ là
| A. $4$. | B. $7$. |
| C. $3$. | D. $5$. |
Lời giải
Ta có: $\left| z \right| = \sqrt {{3^2} + {4^2}} = 5$.
Chọn D.
Câu 20. Tìm phần ảo của số phức $z$ biết $\left( {1 + 2i} \right)z = 3 – 4i$.
| A. $ – 2$. | B. $2$. |
| C. $4$. | D. $ – 4$. |
Lời giải
Ta có:$\left( {1 + 2i} \right)z = 3 – 4i \Leftrightarrow z = \dfrac{{3 – 4i}}{{1 + 2i}} = – 1 – 2i$.
Chọn A.
Câu 21. Trên mặt phẳng tọa độ điểm biểu diễn của số phức $z = 1 – 3i$ là điểm nào dưới đây?
| A. $Q\left( {1;3} \right)$. | B. $P\left( {1; – 3} \right)$. |
| C. $N\left( { – 1;3} \right)$. | D. $M\left( { – 1; – 3} \right)$. |
Lời giải
Chọn B.
Câu 22. Trong không gian $Oxyz$, cho điểm $M(2;0; – 1)$. Mệnh đề nào sau đây đúng?
| A. $M \in (Oxz)$. | B. $M \in (Oyz)$. |
| C. $M \in Oy$. | D. $M \in (Oxy)$. |
Lời giải
Chọn A
Câu 23. Trong không gian $Oxyz$ cho mặt cầu $\left( S \right):{\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 1} \right)^2} = 2$. Tâm của $\left( S \right)$có tọa độ là
| A. $\left( {3\,;\, – 1\,;\,1} \right)$. | B. $\left( { – 3\,;\, – 1;\,1} \right)$. |
| C. $\left( { – 3;\,1\,; – \,1} \right)$. | D. $\left( {3\,;\,1\,;\, – 1} \right)$. |
Lời giải
Chọn B
Câu 24. Trong không gian $Oxyz,$cho mặt phẳng $\left( P \right):2x – y + 6 = 0$. Vectơ nào dưới đây là một vectơ pháp tuyến của $\left( P \right)$?
| A. ${\vec n_3} = (2;1;0)$. | B. ${\vec n_1} = (2; – 1;6)$. |
| C. ${\vec n_2} = (2; – 1;0)$. | D. ${\vec n_4} = (2;1;6)$. |
Lời giải.
Chọn C
Câu 25. Trong không gian $Oxyz$, phương trình nào dưới đây là phương trình của đường thẳng đi qua điểm $A(2;3;0)$ và vuông góc với mặt phẳng $(P):x + 3y – z + 5 = 0?$
| A. $ \left\{ \begin{gathered} x = 1 + t \hfill \\ y = 3t \hfill \\ z = 3 – t \hfill \\\end{gathered} \right.$. | B. $\left\{ \begin{gathered} x = 1 + 2t \hfill \\ y = 3 + 3t \hfill \\ z = – 1 \hfill \\\end{gathered} \right.$. |
| C. $\left\{ \begin{gathered} x = 1 + t \hfill \\ y = 1 + 3t \hfill \\ z = 1 – t \hfill \\\end{gathered} \right.$. | D. $\left\{ \begin{gathered} x = 1 + t \hfill \\ y = 3t \hfill \\ z = 1 – t \hfill \\\end{gathered} \right.$. |
Lời giải
Đường thẳng $d$ đi qua $A(2;3;0)$ nên loại A, B, C. Chọn D.
Nguồn đề: Sưu tầm
About Bitex Khánh Vũ
