BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI CÁC CÂU VẬN DỤNG TRONG ĐỀ THI THỬ NGÀY 10/07/2020
- 20/07/2020
- 80 lượt xem
Nhằm giúp các bạn ôn luyện tốt hơn, thay vì chỉ đăng đáp án như trước thì đợt này Diễn đàn sẽ thực hiện giải một số câu trong đề thi trên máy tính Casio fx-580VN X. Hị vọng nó sẽ giúp ích được các bạn trong kì thi tuyển sinh THPT QG 2020 sắp tới. Trong bài viết này Diễn đàn sẽ thực hiện giải từ câu 26 đến câu 40 của đề thi.
LINK: http://bitexedu.com/de-thi-thu-ngay-10-07-2020/
Câu 26. Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$, $SA = \sqrt 2 a$, tam giác $ABC$ vuông cân tại $B$ và $AC = 2a$ (xem hình bên). Góc giữa đường thẳng $SA$ và mặt phẳng $(SBC)$ bằng
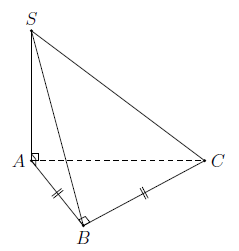
| A. ${30^\circ }$. | B. ${45^\circ }$. |
| C.${60^\circ }$. | D.${90^\circ }$. |
Lời giải
Gán hệ trục tọa độ ta được: $S\left( {0;0;a\sqrt 2 } \right);A\left( {0;0;0} \right);B\left( {0;a\sqrt 2 ;0} \right);C\left( {a\sqrt 2 ;a\sqrt 2 ;0} \right)$
Như vậy ta được $\overrightarrow {SA} = \left( {0;0; – a\sqrt 2 } \right);\overrightarrow {SB} = \left( {0;a\sqrt 2 ; – a\sqrt 2 } \right);\overrightarrow {SC} = \left( {a\sqrt 2 ;a\sqrt 2 ; – a\sqrt 2 } \right)$
Nhập tọa độ vào phương thức vector
Tính Vector pháp tuyến của mặt phẳng $\left( {SBC} \right)$: $\overrightarrow {{n_{SBC}}} = \left[ {\overrightarrow {SB} ,\overrightarrow {SC} } \right] = \left( {0; – 2; – 2} \right)$
Vậy góc giữa $SA$và mặt phẳng $\left( {SBC} \right)$ là:
$\sin \alpha = \dfrac{{\left| {\overrightarrow {SA} .\overrightarrow {{n_{SBC}}} } \right|}}{{\left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {{n_{SBC}}} } \right|}} = \dfrac{{\sqrt 2 }}{2}$
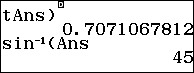
Ta chọn câu B.
Câu 27. Cho hàm số $f(x)$ có đạo hàm trên $\mathbb{R}$ và có dấu của $f'(x)$ như sau
Hàm số $y = f(2 – x)$ có bao nhiêu điểm cực trị
| A. $3$. | B. $1$. |
| C. $2$. | D. $4$. |
Lời giải
Dựa vào bảng xét dấu, $f(x)$ có ba điểm cực trị. Ta thấy đồ thị hàm $f(2 – x)$ thu được bằng cách lấy đối xứng đồ thị hàm số $f(x)$ qua gốc tọa độ $O$, rồi tịnh tiến sang trái $2$ đơn vị, do đó đồ thị hàm số hàm số $f(2 – x)$ cũng có $3$ điểm cực trị. Chọn A.
Câu 28. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = {x^3} – 3{x^2} – 9x + 35$ trên đoạn $[ – 4;4]$ lần lượt là
| A. $40$ và $8$. | B. $40$ và $ – 8$. |
| C. $15$ và $ – 41$. | D. $40$ và $ – 41$. |
Lời giải
Sử dung máy tính để tìm cực trị của hàm số:
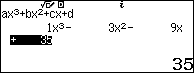
Tính $y\left( { – 4} \right);y\left( 4 \right)$:
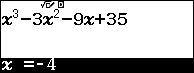
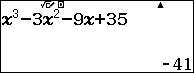
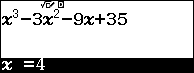
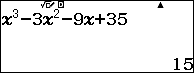
Vậy $\mathop {\min }\limits_{[ – 4;4]} y = y( – 4) = – 41$ và $\mathop {\max }\limits_{[ – 4;4]} y = y( – 1) = 40$. Chọn D.
Câu 29. Xét các số thực $a$ và $b$ thỏa mãn ${\log _2}\left( {{2^a} \cdot {{128}^b}} \right) = {\log _{2\sqrt 2 }}2$. Mệnh đề nào dưới đây là đúng?
| A. $3a + 21b = 2$. | B. $a + 7b = 1$. |
| C. $a + 7b = 7$. | D. $3a + 21b = 4$. |
Lời giải
Do
Nên đẳng thức đã cho tương đương với
${\log _2}\left( {{2^a} \cdot {2^{7b}}} \right) = \dfrac{2}{3} \Leftrightarrow a + 7b = \dfrac{2}{3} \Leftrightarrow 3a + 21b = 2.$
Chọn A.
Câu 30. Cho hàm số $y = {x^3} + mx + 2$ có đồ thị $({C_m})$. Tìm tất cả các giá trị $m$ để đồ thị $({C_m})$ cắt trục hoành tại một điểm duy nhất.
| A. $m < – 3$. | B. $m \leqslant 0$. |
| C. $m \geqslant 0$. | D. $m > – 3$. |
Lời giải
Để giảm thiểu thời gian thực hiện bài toán, ta sử dụng thử đáp án để giải bài toán
Ta kiểm tra với giá trị $m = 5$:
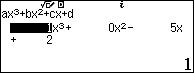
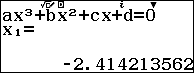
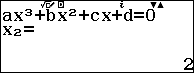
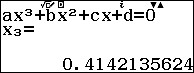
Do phương trình có 3 nghiệm phân biệt nên ta loại được đáp án A,B.
Tiếp tục thực hiện với $m = – 2$
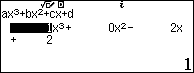
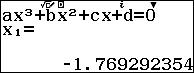
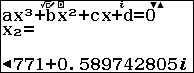
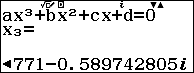
Như vậy ta thấy phương trình có một nghiệm thực và 2 nghiệm phức, tức là hàm số $y = {x^3} – 2x + 2$ cắt trục hoành tại 1 điểm. Nên ta loại được C, chọn D.
Câu 31. Gọi $a$ và $b$ là nghiệm nguyên lớn nhất và nhỏ nhất của bất phương trình $latex {{2.5}^{{x+2}}}+{{5.2}^{{x+2}}}<133.\sqrt{{{{{10}}^{x}}}}$. Khi đó $A=a-b$ có giá trị bằng
| A. $-4$. | B. $6$. |
| C. $-6$. | D. $4$. |
Lời giải
Biến đổi phương trình đã cho ta được:
${2.5^{x + 2}} + {5.2^{x + 2}} < 133\sqrt {{{10}^x}}$
$ \Leftrightarrow {50.5^x} – 133\sqrt {{{10}^x}} + {20.2^x} < 0$
$ \Leftrightarrow 50{\left( {{{\sqrt {\dfrac{5}{2}} }^x}} \right)^2} – 133\left( {{{\sqrt {\dfrac{5}{2}} }^x}} \right) + 20 < 0$
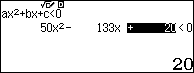
Vậy $\dfrac{4}{{25}} < {\sqrt {\dfrac{5}{2}} ^x} < \dfrac{5}{2} \Leftrightarrow – 4 < x < 2$
Vậy $a = 1;b = – 3 \Rightarrow a – b = 4$, ta chọn D.
Câu 32. Trong không gian cho tam giác $ABC$ vuông tại $A$ có $AB = \sqrt 3 $ và $\widehat {ACB} = {30^{\text{o}}}$. Khi quay tam giác $ABC$ xung quanh cạnh $AC$thì đường gấp khúc $ACB$ tạo thành một hình nón. Diện tích toàn phần của hình nón đó bằng.
| A. $9\pi $. | B. $3\pi $. |
| C. $3\sqrt 3 \pi $. | D. $\sqrt 3 \pi $. |
Lời giải
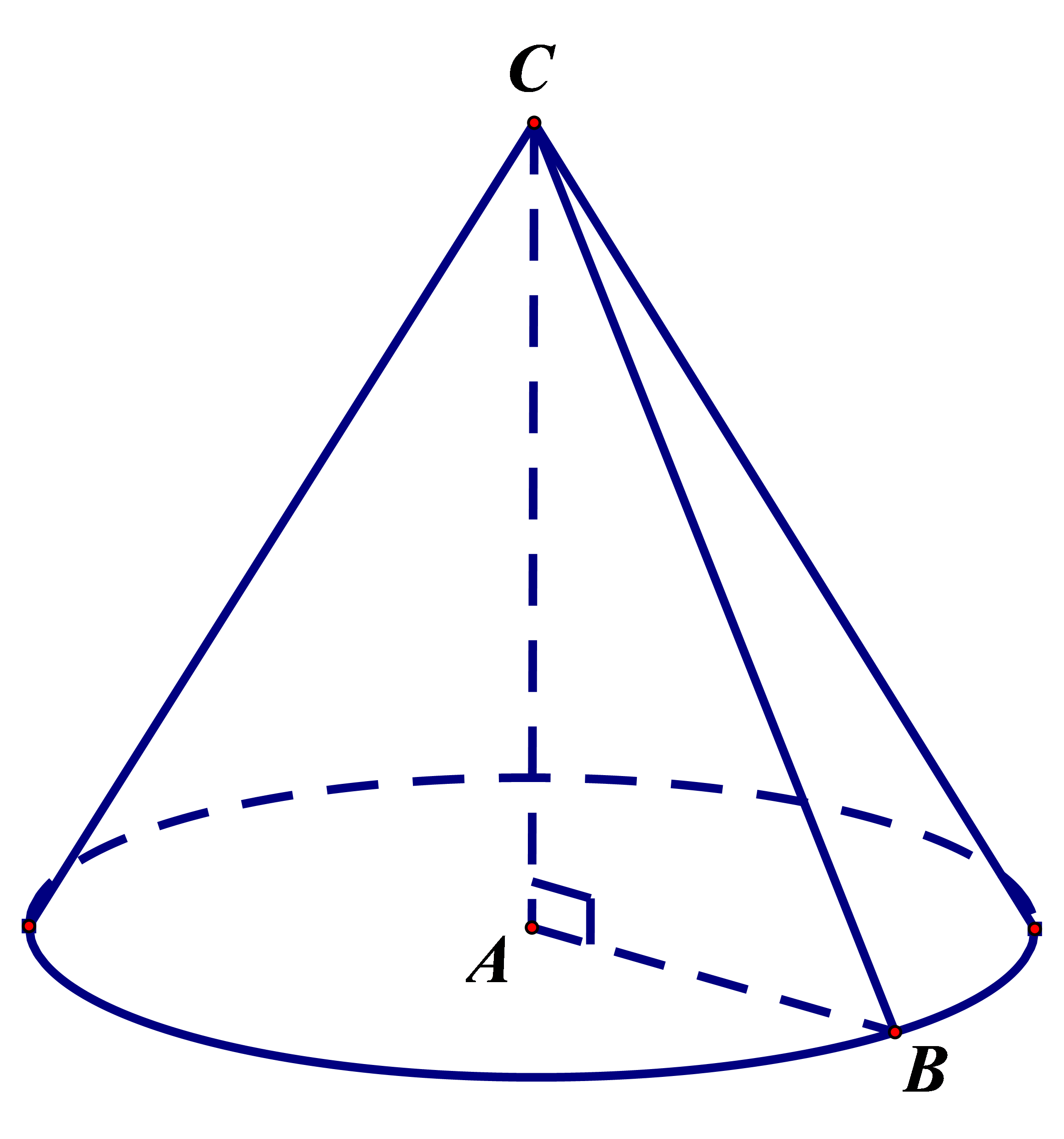
Quay tam giác $ABC$ quanh cạnh $AC$ ta được khối nón có:
+ Đường sinh $l = BC = \dfrac{{AB}}{{\sin {{30}^0}}} = 2\sqrt 3 .$
+ Bán kính đáy $r = AB = \sqrt 3 .$
Diện tích toàn phần của hình nón:
$S_{T P}=S_{X q}+S_{D a y}=\pi r l+\pi r^{2}=\pi r(l+r)=\pi \cdot \sqrt{3}(2 \sqrt{3}+\sqrt{3})=9 \pi$
Chọn A.
Câu 33. Cho $I = \int\limits_0^{\frac{\pi }{2}} {{{\sin }^2}x{{\cos }^2}xdx} $ và $u = \sin x$. Mệnh đề nào dưới đây đúng?
| A. $I = \int_0^1 {\left( {{u^2} – {u^4}} \right)} {\text{d}}u$ | B. $I = 2\int_0^1 {\left( {{u^2} – {u^4}} \right)} {\text{d}}u$ |
| C. $I = \int_0^1 {\left( {{u^4} – {u^2}} \right)} {\text{d}}u$ | D. $I = – \int_0^1 {{u^2}} {\text{d}}u$ |
Lời giải
Ta có:
$I = \int_0^{\frac{\pi }{2}} {{{\sin }^2}} x{\cos ^3}x{\text{d}}x = \int_0^{\frac{\pi }{2}} {{{\sin }^2}} x\left( {1 – {{\sin }^2}x} \right)\cos x{\text{d}}x$
Đặt $u = \sin x \Rightarrow du = \cos xdx$
Đổi cận : $x = 0 \Rightarrow u = 0;x = \dfrac{\pi }{2} \Rightarrow u = 1$
Vậy $I = \int_0^1 {\left( {{u^2} – {u^4}} \right)} {\text{d}}u$. Chọn A.
Câu 34. Diện tích $S$ của hình phẳng giới hạn bởi đồ thị các hàm số $y = – {x^2} – x + 1,\,\,$$y = 2$, $x = – 1$, $x = 1$ được tính bởi công thức nào dưới đây?
| A.$S = \int\limits_{ – 1}^1 {( – {x^2}} – x + 3){\text{d}}x$. | B. $S = \int\limits_{ – 1}^1 {( – {x^2}} – x – 1){\text{d}}x$. |
| C. $S = \int\limits_{ – 1}^1 {( – {x^2}} – x + 1){\text{d}}x$. | D. $S = \int\limits_{ – 1}^1 {({x^2}} + x + 1){\text{d}}x$. |
Lời giải
Chọn D
Diện tích cần tìm là: $S = \int\limits_{ – 1}^1 {\left| { – {x^2} – x + 1 – 2} \right|} {\text{d}}x$$ = \int\limits_{ – 1}^1 {({x^2}} + x + 1){\text{d}}x$.
Câu 35. Cho hai số phức ${z_1} = 2 – 4i$ và ${z_2} = 1 – 3i.$ Phần ảo của số phức ${z_1} + i\overline {{z_2}} $bằng
| A. $5$. | B. $3i$. |
| C. $ – 5i$. | D. $ – 3$. |
Lời giải
Chọn D
Sử dụng máy tính
Vậy phần ảo của số phức ${z_1} + i\overline {{z_2}} $ là $ – 3$.
Câu 36. Gọi ${z_1},{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {z_2}$ nghiệm của phương trình ${z^2} + 4z + 5 = 0$. Tìm $w = {\left( {1 + {z_1}} \right)^{100}} + {\left( {1 + {z_2}} \right)^{100}}.$
| A. $w = {2^{50}}i$. | B. $w = – {2^{51}}$. |
| C. $w = {2^{51}}$. | D. $w = – {2^{50}}i$. |
Lời giải
Chọn B
Sử dụng máy tính để giải phương trình
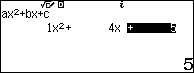
Ta lưu nghiệm ${x_1}$ vào A và ${x_2}$ vào B
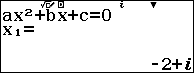
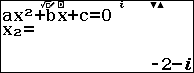
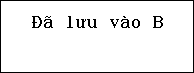
Sau đó qua phương thức số phức thực hiện tính $w$ sau đó lưu vào C
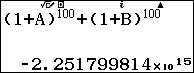
Thử đáp án A,
Loại đáp án A, ta thử tiếp đáp án B:
Nhận, vậy chọn đáp án B.
Câu 37. Viết đường thẳng $\Delta $ nằm trong mặt phẳng $(P):2x – y – z + 4 = 0$ và vuông góc với đường thẳng $d:\dfrac{x}{1} = \dfrac{{y – 1}}{2} = \dfrac{{z + 2}}{{ – 3}} \cdot $ Biết $\Delta $ đi qua điểm $M(0;1;3).$
| A. $\Delta :\dfrac{x}{1} = \dfrac{{y – 1}}{{ – 1}} = \dfrac{{z – 3}}{1}$. | B. $\Delta :\dfrac{x}{1} = \dfrac{{y – 1}}{1} = \dfrac{{z – 3}}{1}$. |
| C. $\Delta :\dfrac{x}{1} = \dfrac{{y + 1}}{{ – 1}} = \dfrac{{z + 3}}{1}$. | D. $\Delta :\dfrac{x}{1} = \dfrac{{y + 1}}{1} = \dfrac{{z + 3}}{1}$. |
Lời giải.
Chọn B
Do $M \in \Delta $ nên ta loại C,D.
Do ${\vec u_\Delta } = {\text{[}}{\vec n_{(P)}},{\vec u_d}] = \left( {5;5;5} \right)$ nên ta loại A, ta chọn B.
Câu 38. Cho điểm $A(1;2;3)$ và đường thẳng $d:\dfrac{{x + 1}}{1} = \dfrac{y}{{ – 2}} = \dfrac{{z – 1}}{3} \cdot $ Viết phương trình đường thẳng $\Delta $ đi qua $A,$ vuông góc và cắt $d.$
| A. $\dfrac{{x – 1}}{6} = \dfrac{{y – 2}}{9} = \dfrac{{z – 3}}{4}$. | B. $\dfrac{{x – 1}}{{23}} = \dfrac{{y – 2}}{{ – 19}} = \dfrac{{z – 3}}{{13}}$. |
| C. $\dfrac{{x – 1}}{{23}} = \dfrac{{y – 2}}{{19}} = \dfrac{{z – 3}}{{ – 13}}$. | D. $\dfrac{{x + 1}}{{23}} = \dfrac{{y + 2}}{{19}} = \dfrac{{z + 3}}{{13}}$ |
Lời giải.
Do đường thẳng $\Delta $ đi qua $A,$nên ta loại D.
Do $d$ vuông góc với $\Delta $ nên ta thử các đáp án
Ta loại được B,C, ta chọn A.
Câu 39. Hai bạn A và B mỗi bạn viết ngẫu nhiên một số tự nhiên gồm ba chữ số đôi một khác nhau. Xác suất để các chữ số có mặt ở hai số bạn A và B viết giống nhau bằng
| A. $\dfrac{{31}}{{2916}}$. | B. $\dfrac{1}{{648}}$. |
| C. $\dfrac{1}{{108}}$. | D. $\dfrac{{25}}{{2916}}$. |
Lời giải.
Mỗi bạn có $9.A_9^2$ cách viết nên số phần tử của không gian mẫu là $n\left( \Omega \right) = {\left( {9.A_9^2} \right)^2}$.
Ta tìm cách viết mà các chữ số các chữ số có mặt trong hai số mà bạn A và B viết giống nhau Bạn A có tất cả $9.A_9^2$cách viết, trong đó $A_9^3$ cách viết mà số không gồm chữ số $0$ và có $\left( {9.A_9^2 – A_9^3} \right)$ cách viết mà số có chữ số 0.
TH1: Nếu A viết số không gồm chữ số $0$có $A_9^3$ cách, lúc này B có $3!$ cách viết.
TH2: Nếu A viết số có chữ số $0$có $\left( {9.A_9^2 – A_9^3} \right)$ cách, lúc này B có $4$ cách viết.
Vậy có $A_9^3.3! + \left( {9.A_9^2 – A_9^3} \right).4$cách viết thỏa mãn.
Xác suất cần tính bằng $\dfrac{{A_9^3.3! + \left( {9.A_9^2 – A_9^3} \right).4}}{{{{\left( {9.A_9^2} \right)}^2}}} = \dfrac{{25}}{{2916}}$.
Chọn D.
Câu 40. Cho hình chóp $S.ABC$ có đáy ABC là tam giác vuông cân tại $A,$ mặt bên $(SBC)$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. khoảng cách giữa hai đường thẳng $SA$ và $BC$ bằng
| A. $\dfrac{{a\sqrt 3 }}{4}$. | B. $\dfrac{{a\sqrt 2 }}{4}$. |
| C. $\dfrac{{a\sqrt 5 }}{4}$. | D. $\dfrac{{a\sqrt 3 }}{3}$ |
Lời giải.
Ghép hệ trục tọa độ, ta được:
$H\left( {0;0;0} \right);S\left( {0;0;\dfrac{{a\sqrt 3 }}{2}} \right);B\left( { – \dfrac{a}{2};0;0} \right);C\left( {\dfrac{a}{2};0;0} \right);A\left( {0;\dfrac{a}{2};0} \right)$
Như vậy ta có: $\overrightarrow {SA} = \left( {0;\dfrac{a}{2}; – \dfrac{{a\sqrt 3 }}{2}} \right);\overrightarrow {BC} = \left( {a;0;0} \right);\overrightarrow {SB} = \left( { – \dfrac{a}{2};0; – \dfrac{{a\sqrt 3 }}{2}} \right)$
Nhập 2 vector vào máy tính:
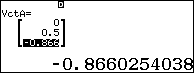
Từ đó, góc giữa SA và BC được tính bằng công thức:
$d\left( {SA,BC} \right) = \dfrac{{\left| {\overrightarrow {SB} \cdot \left[ {\overrightarrow {SA} ,\overrightarrow {BC} } \right]} \right|}}{{\left| {\left[ {\overrightarrow {SA} ,\overrightarrow {BC} } \right]} \right|}} = \dfrac{{a\sqrt 3 }}{4}$
Ta chọn A.
Nguồn: Sưu tầm
About Bitex Khánh Vũ
