Câu 4

Nhập hàm số $P=g(x)$ vào máy tính CASIO fx-880BTG

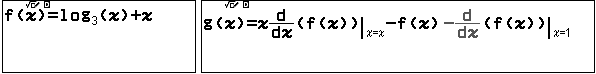
a) Giá trị của biểu thức $P$ tại $x=\dfrac{1}{27}$ bằng

b) Để giải bất phương trình ta điều chỉnh hàm $g(x)$ như sau: cộng thêm $1$ vào hàm $g(x)$ cũ: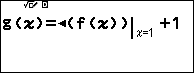

Mở chế độ lập bảng, chọn phạm vi của bảng 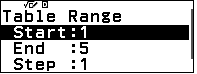, chọn loại bảng một hàm $g(x)$ và cuối cùng ta có két quả về nghiệm nguyên của bất phương trình $P+1<0$ như trong bảng:
, nghĩa là có 4 nghiệm nguyên thuộc đoạn đã cho.

c) Để giải phương trình ta điều chỉnh hàm $g(x)$ như sau: thay $1$ bởi $2$ ta có hàm $g(x)$ mới, thay phạm vi của bảng từ 0 đến 44 với Step bằng 1 ta có bảng phác thảo kết quả: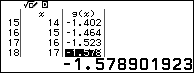

Quan sát nhanh ta thấy hàm số đơn điệu giảm do đó phương trình có một nghiệm duy nhất $x=3$

Tuy nhiên đối với HS khá/giỏi, ta có thể chính xác hóa biểu thức của hàm $P$ như sau:
$$P=x\left(\dfrac{1}{x\ln 3}+1\right)-\log_3x-x-\left(\dfrac{1}{\ln3}+1\right)$$

thu gọn ta có $P=-\log_3x-1$, đây là một hàm đơn điệu giảm như đã nhận xét ở trên.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.