BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
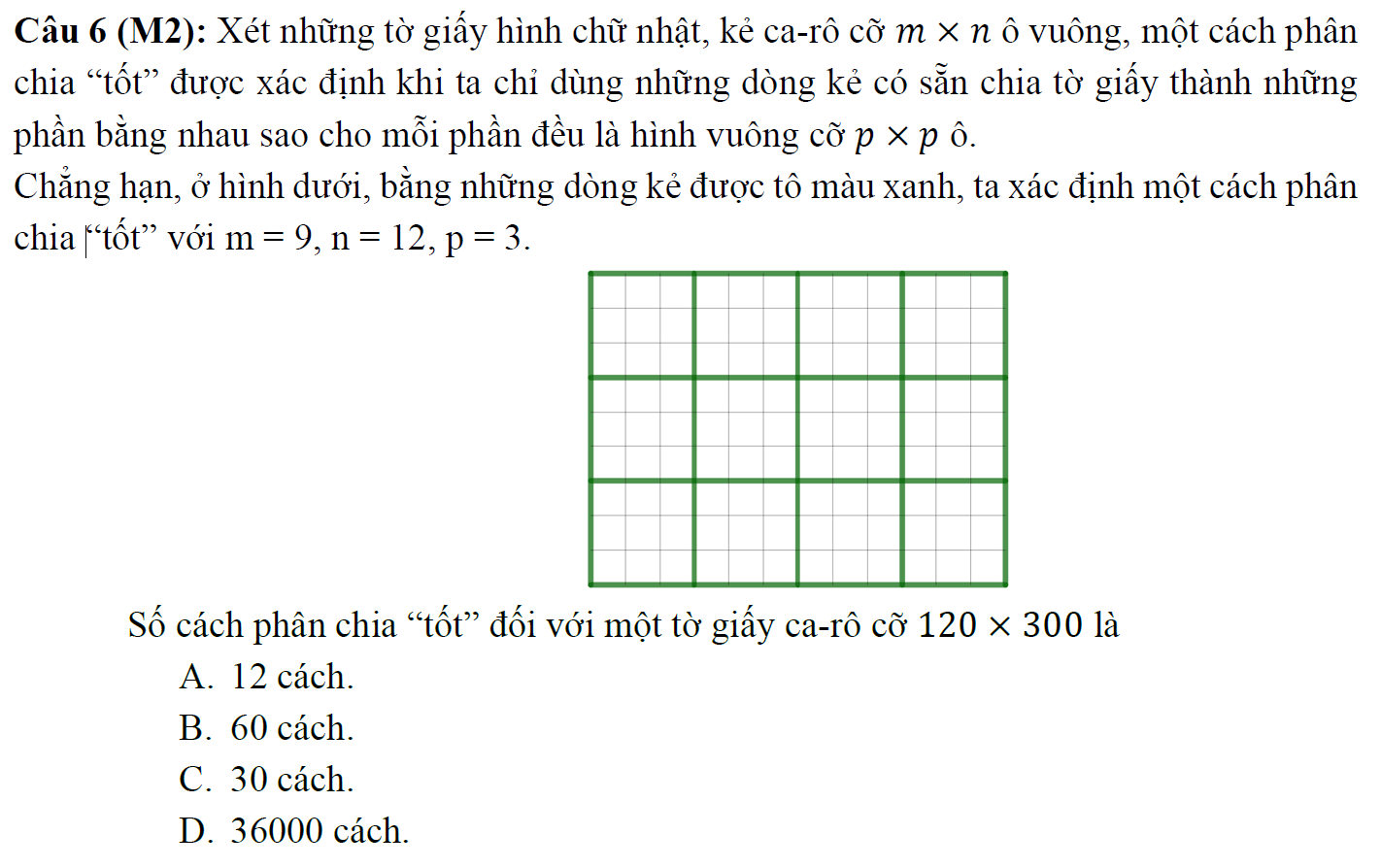
Câu 6
- 03/02/2023
- 45 lượt xem
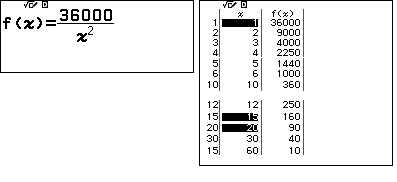
| Gọi $x$ là cạnh hình vuông của phép phân chia tốt. Điều kiện $x$ nguyên và thỏa $1\leqslant x\leqslant \sqrt{36000}\approx 189,7$.
Ta xác định $x$ sao cho $f(x)=\dfrac{36000}{x^2}$ nhận giá trị nguyên (đó là số các hình vuông tạo thành). Sử dụng máy tính Casio fx-880BTG chế độ lập bảng một hàm số $f(x)=\dfrac{36000}{x^2}$ với phạm vi của $x$ từ 1 đến 189 (lần lượt cho phạm vi 1 đến 45, sau đó 46 đến 60). Bạn đọc tự giải thích vì sao nếu $x$ từ 61 đến 189 sẽ không thỏa ycbt.
Ta chọn đáp án A với 12 cách phân chia. |
Chia sẻ
About TS. Nguyễn Thái Sơn
