Hình học không gian

GIẢI

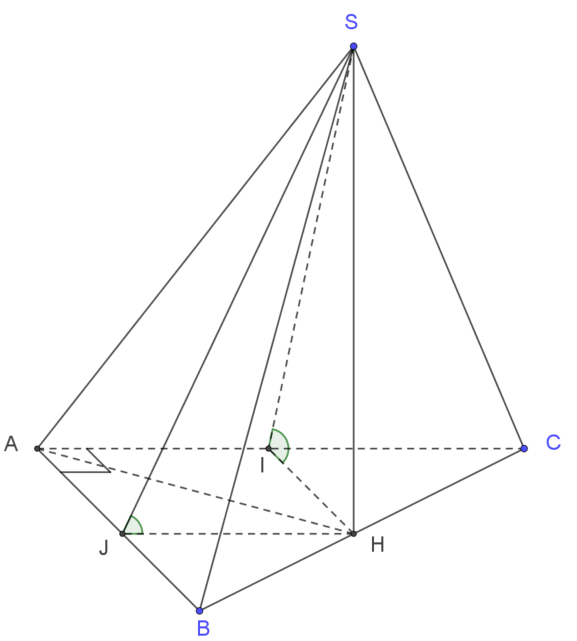
Vì $(SBC)\perp (ABC)$ và cắt nhau theo giao tuyến $BC$ nên ta hạ $SH\perp$ suy ra $SH\perp (ABC)$, nghĩa là $SH$ là đường cao của hình chóp. Vì tam giác $SBC$ nhọn nên $H$ thuộc đoạn $BC$.

Hạ $HI\perp AC$. Vì $AC\perp HI, AC\perp SH$ nên $AC\perp SI$. Vậy $\widehat{SIH}=60^\circ$ là góc tạo bởi hai mặt phẳng $(SAC)$ và $(ABC).

Tương tự $\widehat{SJH}=60^\circ$ là góc tạo bởi hai mặt phẳng $(SAB)$ và $(ABC).

Ta có nhận xét $HI=HJ$ nên $AIHJ$ là hình vuông. Gọi $x$ là cạnh hình vuông ($0\leqslant x\leqslant a$).

Ta có phương trình $$\sqrt{x^2+(2a-x)^2}+\sqrt{x^2+(a-x)^2}=a\sqrt{5}$$

(Do $HC +HB=BC$).

Giải phương trình vô tỉ ta được nghiệm duy nhất $x=\dfrac{2a}{3}$.

Do đó $SH=\dfrac{2a}{3}.\tan 60^\circ=\dfrac{2a\sqrt3}{3}$.

Vậy $$V=\dfrac13.Bh=\dfrac13.\dfrac12.a.2a.\dfrac{2a\sqrt3}{3}=\dfrac{2a^3\sqrt3}{9}$$

Vì $HI=HJ$ nên $AH$ là đường phân giác. Ta có: $$AH=\dfrac{2.AB.AC\sin\dfrac{A}{2}}{AB+AC}=\dfrac{2a\sqrt2}{2}$$ 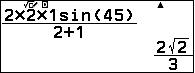Do đó: $HI=\dfrac{AH}{\sqrt2}=\dfrac{2a}{3}$

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.