Giải bài toán Hình học của Thầy Đang Nguyễn
- 11/03/2020
- 629 lượt xem
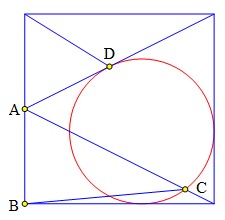
Nhìn hình vẽ không nghĩ bài toán làm khó nhau đến thế.
Chứng minh tứ giác ABCD nội tiếp và tính BC/AD.
Không biết có bao nhiêu người làm được bài này?
P/s tỷ số này họ hàng với tỷ số vàng
———————————————————————–
Chọn hệ trục toạ độ gốc $B$ tia $Bx$ đi qua đỉnh bên phải của hình vuông và tia $By$ đi qua $A$, chọn cạnh hình vuông làm 1 (đvd).
Áp dụng công thức tìm toạ độ tâm đường tròn nội tiếp ta có tâm $I\left(\dfrac{\sqrt5-1}{2};\dfrac{3-\sqrt5}{2}\right)$.
Phương trình đường tròn $$\left(x-\dfrac{\sqrt5-1}{2}\right)^2+\left(y-\dfrac{3-\sqrt5}{2}\right)^2-\dfrac{7-3\sqrt5}{2}=0\qquad (1)$$
Khi đó $AD^2=\dfrac14$ (thay toạ độ điểm $A\left(0;\dfrac12\right)$ vào vế trái phương trình (1)).
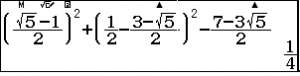
phương trình đường thẳng $AC$ theo đoạn chắn là $x+2y=1 \qquad (2)$.
Giải hệ phương trình (1) (2) ta được $x_C=\dfrac{\sqrt5+2}{5}$.
$BC^2=x_C^2+y_C^2=\left(\dfrac{3\sqrt5-5}{2}\right)x_C=\dfrac{\sqrt5+5}{10}$. 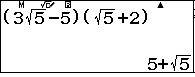
Vậy $\dfrac{BC}{AD}=2BC=\sqrt{2\left(1+\dfrac{\sqrt5}{5}\right)}$.
PS. Việc thu gọn các căn thức để cho kết quả đẹp được thực hiện trên máy tính casio fx-580 VNX.
Một cách khác tính $BC^2$ như sau: $y_C=\dfrac{1-x_C}{2}=\dfrac{3-\sqrt5}{10}$
Vậy $x_C^2+y_C^2=\dfrac{9+4\sqrt5}{25}+\dfrac{14-6\sqrt5}{100}=\dfrac{5+\sqrt5}{10}$. 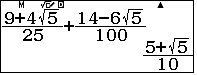
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay