Câu 47 (mã đề 101), chứng minh phương trình vô nghiệm khi $\mathbf{y \geqslant 10}$.
- 21/07/2021
- 311 lượt xem
Trên Diễn đàn này chúng tôi đã chỉ ra nghiệm cụ thể khi $y=1,2,3,4,5,6,7,8,9$.
Khi $y=0$ phương trình có hai nghiệm $x=0; x=3$ không thuộc khoảng $\left(\dfrac13;3\right)$.
Khi $y=-2$ hay $y= -1$ phương trình có ít nhất một nghiệm trên khoảng $\left(\dfrac13;3\right)$ (thực ra nghiệm đó là duy nhất).
Bây giờ ta chứng minh khi $y \geqslant 10$ phương trình không có nghiệm trên khoảng $\left(\dfrac13;3\right)$.
Ta có $f(x)=3x^2+(y-9)x-\log_{27}(1+yx)$.
$f'(x)=6x+y-9-\dfrac{y}{(1+yx)\ln27}$
Lấy đạo hàm của $f'(x)$ ta có:
$$f”(x)=6+\dfrac{yx}{(1+yx)^2\ln^227}> 0 \quad \forall x >\dfrac13$$
Vậy $f'(x)$ là hàm số đơn điệu tăng, do dó $f'(x)>f’\left(\dfrac13\right)=g(y)=y-7-\dfrac{3y}{(3+y)\ln 27}$
Ta có $g'(y)=1-\dfrac{9}{((3+y)\ln 27)^2}\geqslant 1-\dfrac{9}{(13\ln 27)^2}>0$ (vì $y\geqslant 10$)
Vậy $f(x)$ là hàm đơn điệu tăng trên khoảng $\left(\dfrac13;3\right)$.
Do đó $f(x)>f\left(\dfrac13\right)=h(y)=\dfrac13+\dfrac{y-9}{3}-\log_{27}(1+\dfrac{y}{3})$
Ta có $h'(y)=\dfrac13-\dfrac{1}{(3+y)\ln 27} \geqslant$  $>0$. Vậy $h(y)$ là hàm đơn điệu tăng nên $h(y) \geqslant h(10)=$
$>0$. Vậy $h(y)$ là hàm đơn điệu tăng nên $h(y) \geqslant h(10)=$ 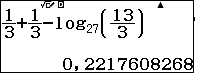
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay