BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI CHI TIẾT CÂU HÌNH NÓN MỨC ĐỘ VẬN DỤNG TRONG ĐỀ THAM KHẢO THPT 2023
- 03/03/2023
- 91 lượt xem
Đề bài: (Câu 48 đề tham khảo THPT 2023) Cho khối nón có đỉnh $S$, chiều cao bằng 8 và thể tích bằng $\dfrac{800\pi }{3}$. Gọi $A$ và $B$ là hai điểm thuộc đường tròn đáy sao cho $AB=12$, khoảng cách từ tâm của đường tròn đến mặt phẳng $(SAB)$ bằng
A. $8\sqrt{2}$ B. $\dfrac{24}{5}$ C.$4\sqrt{2}$ D. $\dfrac{5}{24}$
Lời giải
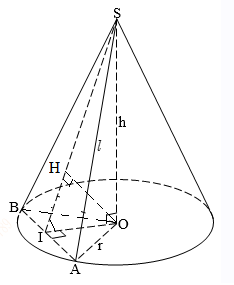
Bước 1: Dựng hình
Kẻ $OI\perp AB$, từ $O$ kẻ đường thẳng vuông góc với $SI$ tại $H$
$\Rightarrow d(O,(SAB))=OH$
Bước 2: Chứng minh $OH\perp (SAB)$
Ta có $\left\{\begin{matrix}OI\perp AB\\SO\perp AB\end{matrix}\right.$
$\Rightarrow AB\perp (SIO)\Rightarrow AB\perp OH$
mà $SI\perp OH$
$\Rightarrow OH\perp (SAB)$
$\Rightarrow d(O,(SAB))=OH$
Bước 3: Tính $OH$
Ta có $V=\dfrac{800\pi }{3}$
$\Leftrightarrow \dfrac{1}{3}\pi .r^2.h=\dfrac{800\pi }{3}$
$\Rightarrow r=10$
Xét $\Delta OAI$ vuông tại $I$
Ta có $OI^{2}+IA^{2}=OA^{2}$ (định lý Pytago)
$\Leftrightarrow OI^{2}=10^2-6^2$
$\Rightarrow OI=8$
Xét $\Delta SIO$ vuôn tại $O$ có $OH$ là đường cao
Ta có $\dfrac{1}{OH^2}=\dfrac{1}{OI^2}+\dfrac{1}{SO^2}$
$\Rightarrow OH=\dfrac{1}{\sqrt{\dfrac{1}{8^2}+\dfrac{1}{8^2}}}=4\sqrt{2}$
Chọn C
Chia sẻ
About Toanbitexdtgd1
