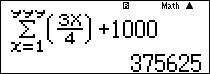Sử dụng phím tổng để tính tổng dãy số
- 25/06/2022
- 1,028 lượt xem
Bài toán: Cho dãy số $(u_n)$ thỏa $u_1=1,\,u_{n+1}=\dfrac{1}{2} \sqrt{4u_n^2+3}$. Tính tổng $S=u_1^2+u_2^2+…+u_{1000}^2$.
- $S=278325$.
- $S=325097$.
- $S=375625$.
- $S=375125$.
Bài giải
Chọn C.
Biến đổi biểu thức có trong dãy số, ta được: $u_{n+1}^2=u_n^2+\dfrac{3}{4}$.
Đặt $v_n=u_n^2$ thu được $v_{n+1}=v_n+\dfrac{3}{4}$.
Vậy $(v_n)$ là một cấp số cộng với $v_1=1,\,d=\dfrac{3}{4}$.
Ta cần tính tổng $S=v_1+v_2+…+v_{1000}$.
Nhập vào màn hình tính tổng:
Chia sẻ
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay