BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tính giá trị biểu thức mũ-logarit
- 17/05/2022
- 194 lượt xem
Phương pháp:
Bước 1: Dựa vào hệ thức điều kiện bắt buộc bài toán chọn giá trị thích hợp cho biến.
Bước 2: Tính các giá trị liên quan đến biến rồi gắn vào $A,B,C$.
Bước 3: Quan sát 4 đáp án và chọn chính xác.
Ví dụ: Cho $a=\log_{27}5; b=\log_87; c=\log_23$. Tính $\log_{12}35$ theo $a,b,c$?
| A. $\dfrac{3b+2ac}{c+2}$ | B. $\dfrac{3b+3ac}{c+2}$ | C. $\dfrac{3b+2ac}{c+3}$ | D. $\dfrac{3b+3ac}{c+1}$ |
Hướng dẫn
Gán các giá trị $\log_{27}5; \log_87; \log_23, \log_{12}35$ lần lượt cho các biến $A, B, C$ và $D$.
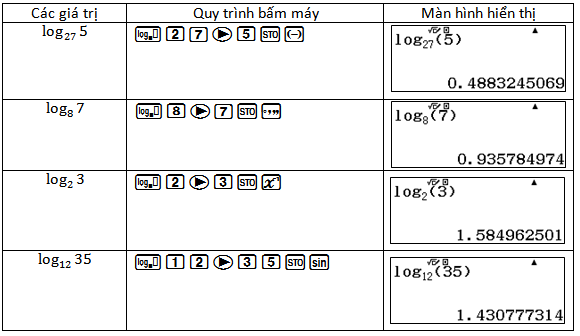
và nhập vào màn hình $D-\dfrac{3B+2AC}{C+2}; D-\dfrac{3B+3AC}{C+2}, D-\dfrac{3B+2AC}{C+3}; D-\dfrac{3B+3AC}{C+1}$. Kết quả bằng $0$ là đáp án đúng.
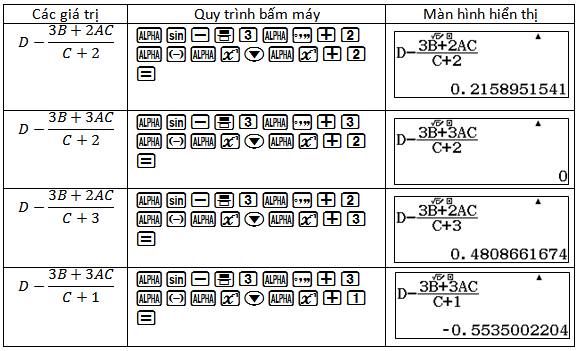
Đáp án B.
Chia sẻ
About Tạ Quang Tuấn
