Định lý Simson và ứng dụng
- 23/05/2022
- 7,035 lượt xem
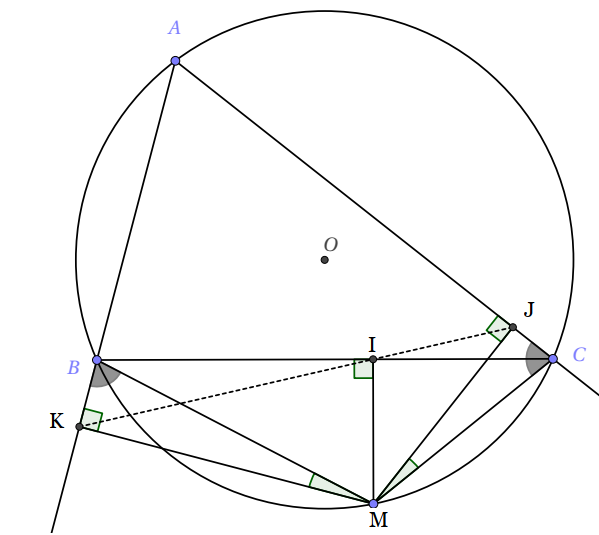
Chứng minh.
- Tứ giáC $MIBK$ nội tiếp đường tròn đường kính $BM$ nên $\widehat{BIK}=\widehat{BMK} =90^\circ -\widehat{MBK}$
- Tứ giáC $MIJC$ nội tiếp đường tròn đường kính $CM$ nên $\widehat{CIJ}=\widehat{CMJ} =90^\circ -\widehat{MCJ}$
- Tứ giáC $ABMC$ nội tiếp đường tròn $(O)$ nên $\widehat{MBK}=\widehat{MCJ}$
Vậy $\widehat{BIK}=\widehat{CIJ}$, suy ra ba điểm $I, J, K$ thẳng hàng. (đpcm).
Áp dụng 1: Đề thi lớp 10 năm 2014 SGD và ĐT Hà Nam.
Cho tam giác ABC có ba góc nhọn và AB>AC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.
- a) Chứng minh tứ giác BDHM nội tiếp đường tròn.
- b) Chứng minh $DA$ là tia phân giác của $\widehat{MDC}$
- c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.
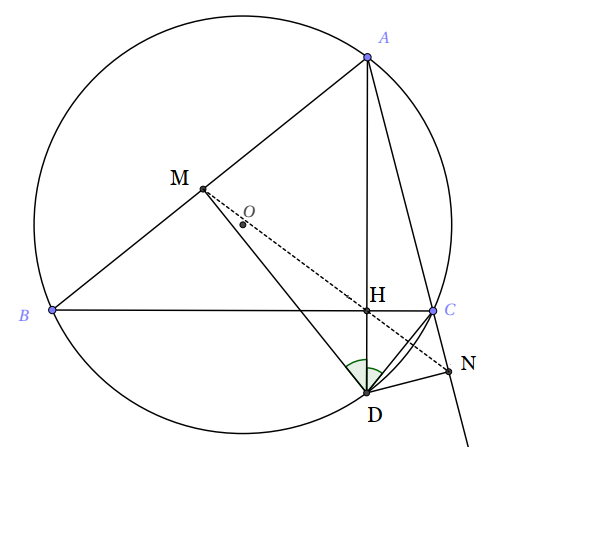
Giải
- a) Ta thấy $M$ và $H$ cùng nhìn $BD$ dưới một góc vuông nên tứ giác $BDHM$ nội tiếp đường tròn đường kính $BD$.
- b) $\widehat{ADC}=\widehat{ABC}$ (cùng chắn cung $AC$)$\widehat{ABC}=\widehat{ADM}$ (góc có các cạnh vuông góc)Suy ra $\widehat{ADC}=\widehat{ADM}$, nghĩa là $DA$ là tia phân giác của $\widehat{MDC}$.
- b) $D$ nằm trên đường tròn ngoại tiếp tam giác $ABC$ và $H, N, M$ lần lượt là hình chiếu vuông góc của $D$ trên các cạnh $BC, CA, AB$ nên ba điểm $H, N, M$ thẳng hàng trên đường thẳng Simson ứng với điểm $D$ của tam giác.
Lưu ý: Thay vì giải thích như trên, học sinh viết 4 dòng của chứng minh vào bài làm.
Áp dụng 2: Đề thi lớp 10 năm 2016 SGD và ĐT Daklak.
Cho điểm M nằm trên nửa đường tròn đường kính AB (M khác A và B), trên cung BM lấy điểm N (N khác B và M). Gọi C là giao điểm của đường thẳng AM và đường thẳng BN, H là giao điểm của đoạn thẳng BM và đoạn thẳng AN. Gọi D là điểm đối xứng của điểm H qua điểm M; P là hình chiếu vuông góc của điểm A lên đường thẳng DC.
- a) Chứng minh CH $\perp$ AB.
- b) Chứng minh tứ giác ABCD nội tiếp.
- c) Chứng minh ba điểm P, M, N thẳng hàng.
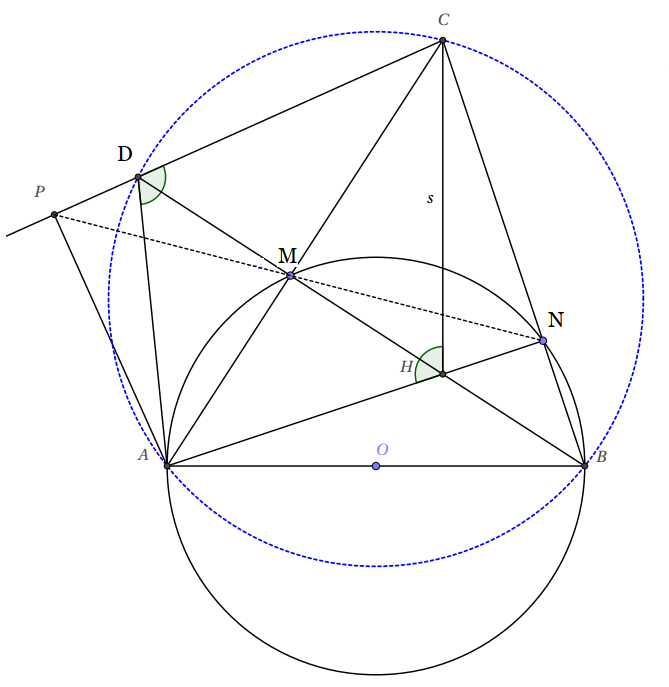
Giải
- a) Tam giác $ABC$ nhận $AN$ và $BM$ làm hai đường cao nên $H$ là trực tâm. Suy ra $CH \perp AB$.
- b) Do $AC$ là đường trung trực của $DH$ nên $\widehat{ADC}=\widehat{CHA}=90^\circ+\widehat{NCH}=90^\circ+90^\circ -\widehat{CBA}$.Suy ra $\widehat{ADC}+\widehat{CBA}=180^\circ$. Do đó tứ giác $ABCD$ nội tiếp.
- c) Điểm $A$ nằm trên đường tròn ngoại tiếp tam giác $BDC$ và $P, M, N$ lần lượt là hình chiếu vuông góc của $A$ trên các cạnh $CD, DB, BC$ nên theo định lý Simson, ba điểm $P, M, N$ thẳng hàng.
Lưu ý: Kết luận ở trên xem như định hướng nhanh cho lời giải, học sinh viết 4 dòng của chứng minh định lý vào bài làm.
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay