Các tính toán trong khối tứ diện, giải bài toán Hình học kỳ thi HSG MTCT

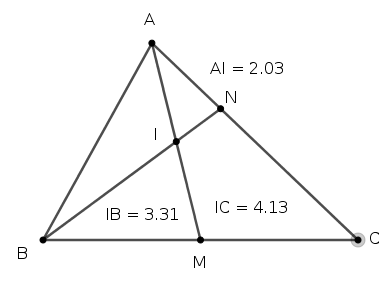
Ta có

$\left.\begin{array}{l}a=\dfrac{CN}{CA}=\dfrac23\\ b=\dfrac{CM}{CB}=\dfrac12\end{array}\right\}\Rightarrow \dfrac{AI}{AM}=\dfrac{1-a}{1-ab}=\dfrac12\quad \text{và}\quad \dfrac{BI}{BN}=\dfrac34.$

Trong đó $AM=\sqrt{\dfrac{AB^2+AC^2-\dfrac{BC^2}{2}}{2}}=$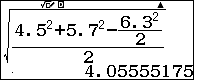lưu vào x.

Suy ra $AI=$. Do đó $SA=$

Ta có:

$BN^2=AB^2+AN^2-2AB.AN.\cos A$ suy ra $BN=$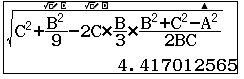

lưu vào y.
Vậy $IB=$. Do đó $SB=$

Cuối cùng ta có $IC^2=BI^2+BC^2-2BI.BC\cos \widehat{NBC}$

suy ra $IC=$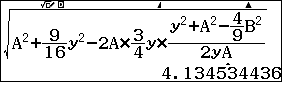

Do đó $SC=$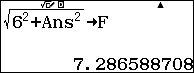

2) Tính chiều cao $BK$ của khối tứ diện $SABC$

$$BK.S_{SAC}=SI.S_{ABC}$$

Dùng công thức Hê-rông tính $S_{SAC}$:

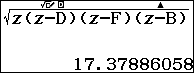lưu vào x.

Dùng công thức Hê-rông tính $S_{ABC}$:

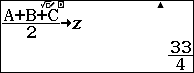
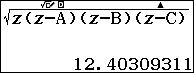lưu vào y.

Vậy $BK=$

c) Tính bán kính $R$ của mặt cầu ngoại tiếp  tứ diện $SABC$.

$$R=\dfrac{S}{6V}$$

trong đó $V$ là thể tích khối  tứ diện $SABC$.

$S$ là “diện tích” của một khối diện có các cạnh là tích của các cặp cạnh đối diện của khối tứ diện $SABC$, cụ thể là ba “cạnh” $D\times a, E\times b, F\times c$.

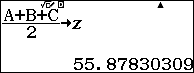
$S=$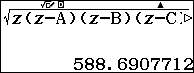

$V=\dfrac13\times 6 y$ 

Kết luận $R=\dfrac{S}{6V}= $

 BÀI TẬP TƯƠNG TỰ VÀ ĐÁP ÁN

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.