Các bài toán xác suất liên quan đến các số tự nhiên được tạo thành
- 11/02/2022
- 131 lượt xem

Ta tính xác suất xảy ra biến cố A theo công thức $$P(A)=\dfrac{|A|}{|\Omega|}$$
trong đó $|\Omega|$ là số phần tử của không gian mẫu, tức là số tất cả các trường hợp có thể xảy ra và $|A|$ là số các trường hợp thuận lợi cho biến cố A.
Để tính số phần tử của $S$ thức là $|\Omega|$ ta chọn 4 chữ số từ 9 chữ số đã cho đặt vào vị trí và hoán vị: $$C^4_9\times 4!=A^4_9$$
Để tính $|A|$ ta có nhận xét rằng không xảy ra trường hợp 3 trong 4 chữ số là chẵn hoặc 4 chữ số đều chẵn. Do đó chỉ xảy ra 3 trường hợp sau đây:
| Trường hợp 1: 4 chữ số đều lẻ. Số các số được thành lập thỏa ycbt là $C^4_5\times 4!$ Trường hợp 2: 3 chữ số đều lẻ và 1 chữ số chẵn. Ta chọn 3 chữ số lẻ từ 5 chữ số lẻ và chọn 1 chữ số chẵn từ 4 chữ số chẵn đặt vào vị trí và hoán vị. Số các số được thành lập thỏa ycbt là $C^3_5\times C^1_4\times 4!$ Trường hợp 3: 2 chữ số đều lẻ và 2 chữ số chẵn. Ta chọn 2 chữ số chẵn từ 4 chữ số chẵn và chọn 2 chữ số lẻ từ 5 chữ số lẻ đặt vào vị trí và hoán vị sau đó bỏ đi các trường hợp 2 chữ số chẵn đứng cạnh nhau. Hai chữ số chẵn đứng cạnh nhau coi như một số đôi, có $A^2_4$ số như vậy, số đôi này cùng với 2 chữ số lẻ đặt vào vị trí và hoán vị. Số các số được thành lập thỏa ycbt là $$C^2_4\times C^2_5\times 4!-A^2_4\times C^2_5\times 3!$$ |
Vậy xác suất cần tìm là: 
| Bài 2: Câu 36 đề thi tham khảo năm 2020. Chọn ngẫu nhiên một số từ tập hợp các số có ba chữ số khác nhau. Tính xác suất để số được chọn có tổng các chữ số là số chẵn. |
Trước hết ta đếm số các số có 3 chữ số khác nhau. Ta chọn 3 chữ số từ 10 chữ số đặt vào vị trí rồi hoán vị, sau đó ta đếm trong những số nói trên có bao nhiêu số bắt dầu bằng 0. Kết quả ta có số các số có 3 chữ số khác nhau bằng $$A^3_{10}-A^2_9$$
Để số được chọn có tổng các chữ số là số chẵn ta xét hai trường hợp.
Trường hợp 1: Ba chữ số đều chẵn: Ta chọn 3 chữ số chẵn từ 5 chữ số chẵn đặt vào vị trí rồi hoán vi, sau đó ta đếm trong những số nói trên có bao nhiêu số bắt đầu bằng 0:$$A^3_5-A^2_4$$
Trường hợp 2: Trong ba chữ số có hai chữ số lẻ và một chữ số chẵn: Ta chọn 2 chữ số lẻ từ 5 chữ số lẻ, chọn 1 chữ số chẵn từ 5 chữ số chẵn đặt vào vị trí và hoán vị, sau đó ta đếm trong những số nói trên có bao nhiêu số bắt đầu bằng 0:$$C^2_5\times C^1_5\times 3!-C^2_5\times 2!$$
Xác suất cần tìm là $$P(A)=\dfrac{(A^3_5-A^2_4)+(C^2_5\times C^1_5\times 3!-C^2_5\times 2!)}{A^3_{10}-A^2_9}$$

| Bài 3:Câu 43 đề thi THPTQG năm 2018. |

Ta có: $P(\Omega)=17^3$.
Ta chia các số tự nhiên từ 1 đến 17 thành 3 loại:
Loại 1: Các số chia hết cho 3 gồm 5 số $\{3,6,9,12,15\}$
Loại 2: Các số chia cho 3 có dư bằng 1 gồm 6 số $\{1, 4,7,10,13,16\}$
Loại 3: Các số chia cho 3 có dư bằng 2 gồm 6 số $\{2,5,8,11,14,17\}$
Để số được chọn có tổng các chữ số chia hết cho 3 ta xét các trường hợp sau:
Trường hợp 1: Ba chữ số đều thuộc loại 1: Ta chọn 3 chữ số (không bắt buộc khác nhau) từ 5 chữ số loại 1 đặt vào vị trí có $5^3$ cách chọn.
Trường hợp 2: Ba chữ số đều thuộc loại 2: như trên có $6^3$ cách chọn.
Trường hợp 3: Ba chữ số đều thuộc loại 3: như trên có $6^3$ cách chọn.
Trường hợp 4: Một chữ số thuộc loại 1, chữ số thuộc loại 2 và một chữ số thuộc loại 3. Ba chữ số này phân biệt, do đó số cách chọn là $5\times 6\times 6\times 3!$.
Vậy xác suất cần tìm là: 
| Bài 4:Đề thi thử Chuyên Vinh lần 3 năm 2019. |

$$P(A)=\dfrac{|A|}{|\Omega|}$$
Số các số tự nhiên có hai chữ số phân biệt $A^2_{10}-A^1_9=$ 
Vậy bạn Công và bạn Thành mỗi bạn có thể viết 81 số do đó $|\Omega|=81^2$.
Gọi $A$ là biến cố hai số được viết ra có ít nhất một chữ số chung. Suy ra $\overline{A}$ là biến cố hai số được viết ra không có chữ số nào chung. Khi đó $\overline{|A|}$ bằng số các số tự nhiên gồm 4 chữ số phân biệt sao cho chữ số thứ ba khác $0$ (và tất nhiên chữ số thứ nhất cũng khác $0$). Chữ số thứ nhất có 9 cách chọn, chữ số thứ ba có 8 cách chọn, hai chữ số còn lại số cách chọn là $A^2_8$.
Vậy xác suất cần tìm $P(A)=1-P(\overline{A})=\quad $ 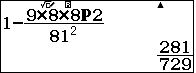
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay