BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Việc lập các số tự nhiên từ các chữ số
- 09/02/2022
- 177 lượt xem
| Từ các chữ số $0,1,2,3,4,5,6,7,8,9$ ta thiết lập các số có $k$ chữ số $k\leqslant 9$ thỏa các điều kiện bổ sung.
Ta bắt đầu từ bài tập của chuyên Lam Sơn (Thanh Hóa) 2022: |
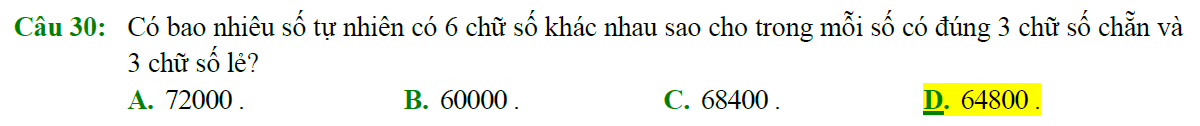
Có nhiều cách thực hiện phép đếm, ở đây chúng tôi gợi ý một cách và thống nhất chỉ dùng một cách duy nhất này để thực hiện phép đếm nhằm giải bài tập ở trên và các bài tập khác cùng chủ đề.
Quy tắc này như sau:
| Bước 1: Ta đếm tất cả các số được tạo thành kể cả những số bắt đầu bằng $0$.
Bước 2: Sau đó ta đếm trong những số ở trên có bao nhiêu số bắt đầu bằng $0$.
Lưu ý: Nếu hai mệnh đề nối với nhau bởi chữ “và” ta dùng quy tắc nhân, hai mệnh đề nối với nhau bởi chữ “hay”, “hoặc” ta dùng quy tắc cộng. |
Ta bắt đầu giải bài toán ở trên.
Trước hết ta chọn 3 chữ số lẻ từ 5 chữ số lẻ và 3 chữ số chẵn từ 5 chữ số chẵn để được 6 chữ số đặt vào vị trí và hoán vị.
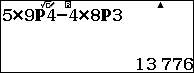
Số cách thực hiện là $C^3_5\times C^3_5\times 6!$
Sau đó ta đếm trong những số nói trên có bao nhiêu số bắt đầu bằng $0$. Không kể số $0$ đứng đầu, ta chọn 3 chữ số lẻ từ 5 chữ số lẻ và 2 chữ số chẵn từ 4 chữ số chẵn (khác 0) để được 5 chữ số đặt vào các vị trí còn lại và hoán vị.
Số cách thực hiện là $C^3_5\times C^2_4\times 5!$
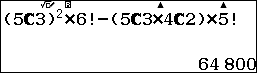
LUYỆN TẬP
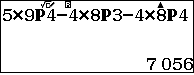
1. Từ các chữ số $0,1,2,3,4,5,6,7,8,9$ có thể lập được bao nhiêu số tự nhiên chẵn, mỗi số gồm 5 chữ số phân biệt.
| Bước 1: Ta đếm tất cả các số được tạo thành kể cả những số bắt đầu bằng $0$.Chọn chữ số đơn vị, có 5 cách chọn, chọn 4 chữ số còn lại, số cách chọn là $C^4_9$, đặt vào vị trí và hoán vị: $$5\times C^4_9\times 4!$$Bước 2: Sau đó ta đếm trong những số ở trên có bao nhiêu số bắt đầu bằng $0$. Chọn chữ số đơn vị, có 4 cách chọn, chọn 3 chữ số còn lại, số cách chọn là $C^3_8$, đặt vào vị trí và hoán vị: $$4\times C^3_8\times 3!$$
Lưu ý: Thay vì thực hiện $C^k_n\times k!$ ta thay bằng $P^k_n$. Vậy: |
2. Từ các chữ số $0,1,2,3,4,5,6,7,8,9$ có thể lập được bao nhiêu số tự nhiên chẵn, mỗi số gồm 5 chữ số phân biệt sao cho mỗi số đó phải có mặt chữ số $0$.
Ta tiến hành như trên nhưng sau đó bỏ thêm các số chẵn có 5 chữ số phân biệt mà không chứa chữ số $0$ (tức là chỉ xét các số $1,2,3,4,5,6,7,8,9$).
| 3. Từ các chữ số $0,1,2,3,4,5,6,7,8,9$ có thể lập được bao nhiêu số tự nhiên chẵn, mỗi số gồm 5 chữ số phân biệt sao cho trong mỗi số đó phải có đúng hai chữ số lẻ và hai chữ số lẻ này không đứng cạnh nhau. |
-
- $–$ Trước hết ta đếm có bao nhiêu số tự nhiên chẵn (kể cả những số bắt đầu bằng $0$), mỗi số gồm 5 chữ số phân biệt sao cho trong mỗi số đó phải có đúng hai chữ số lẻ.Chọn chữ số đơn vị là chữ số chẵn, tiếp theo chọn 2 chữ số lẻ và hai chữ số chẵn đặt vào vị trí và hoán vị (chữ số đơn vị không hoán vị):$$5\times C^2_5\times C^2_4\times 4!$$
- $–$ Sau đó ta đếm trong những số nói trên có bao nhiêu số bắt đầu bằng $0$.
$$4\times C^2_5\times C^1_3\times 3!$$
Vậy số các số tự nhiên chẵn mỗi số gồm 5 chữ số phân biệt sao cho trong mỗi số đó phải có đúng hai chữ số lẻ là:
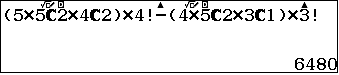
- $–$ Bây giờ ta đếm trong những số vừa tìm có bao nhiêu số mà hai chữ số lẻ đứng cạnh nhau.Hai chữ số lẻ đứng cạnh nhau coi như một số (đôi), có 20 số như vậy vì $A^2_5=20$, thực hiện như trên ta có:
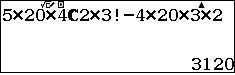
Tóm lại kết quả của bài toán là $$6480-3120=3360$$
About TS. Nguyễn Thái Sơn
