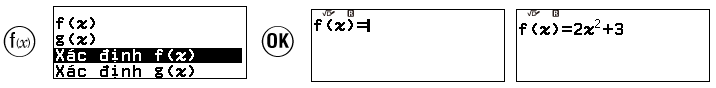BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI CHI TIẾT PHẦN ĐẠI SỐ ĐỀ THI CUỐI KỲ I TRƯỜNG THCS DƯƠNG NỘI - HÀ ĐÔNG
- 08/01/2024
- 39 lượt xem
Câu 1: Biểu thức nào không là đa thức?
A. $9+x^2y$ B. $2xy+xy^2$ C. $-2xz$ D. $3x-2\sqrt{xy}$
Lời giải
Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là hạng tử của đa thức đó.
Ta dễ dang thấy câu $A,B,D$ là những đa thức
Chọn đáp án: A
Câu 2: Giá trị của $x$ thỏa mãn $2(x-1)-3x=0$ là:
A. -2 . B. 2 C. 1 D. -1
Lời giải
Sử dụng tính năng solver trên máy tính Casio Fx-880BTG
Bước 1: Mở tính năng solver
Bước 2: Giải phương trình tìm $x$
Chọn đáp án: A
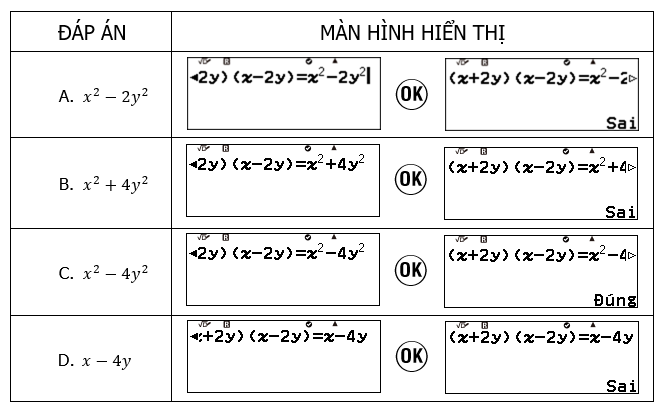
Câu 3: Kết quả của phép tính (x+2y)(x-2y) là:
A. $x^2-2y^2$ B.$ x^2+4y^2$ C. $x^2-4y$ D. $x-4y$
Lời giải
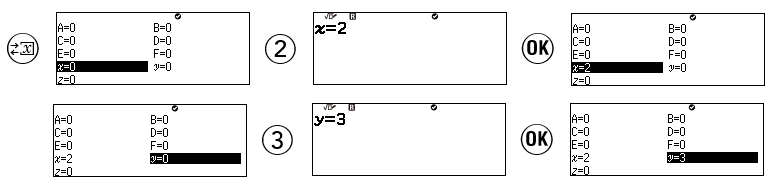
Sử dụng tính năng kiểm tra trên máy tính Casio Fx-880BTG
Bước 1: Bật tính năng kiểm tra
Bước 2: Lưu $x=2$ và $y=3$ (vì nếu không lưu giá trị máy tính sẽ mặc định bằng 0, dẫn đến kết quả kiểm tra bị sai)
Bước 3: Kiểm tra các biểu thức
Chọn đáp án: C
Câu 4: Điều kiện xác định của phân thức $\dfrac{x-3}{2x-6}$ là
A. $x=3$ B. $x\neq -3$ C. $x\neq 3$ D. $x\neq 3$ và $x\neq -3$
Lời giải
Điều kiện xác định của phân thức đại số $\dfrac{A}{B}$ là điều kiện của biến để mẫu $B$ khác $0$
Điều kiện xác định của phân thức $\dfrac{x-3}{2x-6}$ là $2x-6\neq 0$
Sử dụng tính năng solver trên máy tính fx-880BTG giải phương trình $2x-6=0$
Bước 1: Mở tính năng solver
Bước 2: Nhập phương trình và giải phương trình
Vậy điều kiện xác định của phân thức là $x\neq3$
Chọn đáp án: C
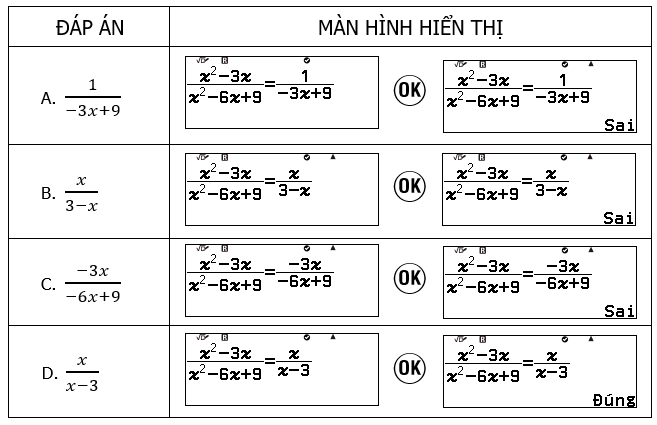
Câu 5: Kết quả rút gọn phân thức $\dfrac{x^2-3x}{x^2-6x+9}$ là:
A. $\dfrac{1}{-3x+9}$ B. $\dfrac{x}{3-x}$ C. $\dfrac{-3x}{-6x+9}$ D. $\dfrac{x}{x-3}$
Lời giải
Sử dụng tính năng kiểm tra trên máy tính Casio Fx-880BTG
Bước 1: Bật tính năng kiểm tra
Bước 2: Lưu $x=2$ (vì nếu không lưu giá trị máy tính sẽ mặc định bằng 0, dẫn đến kết quả kiểm tra bị sai)
Bước 3: Sử dụng tính năng kiểm tra tìm đáp án
Vậy $\dfrac{x^2-3x}{x^2-6x+9}=\dfrac{x}{(x-3)}
Chọn đáp án: D
Câu 6: Cho hàm số $f(x)=2x^2+3$, giá trị của $f(-1)$ là:
A. $5$ B. $1$ C. $-1$ D. $-5$
Lời giải
Bước 1: Sử dụng tính năng Function để lưu hàm số f(x)
Bước 2: Tính $f(-1)$
Vậy $f(-1)=5$
Chọn đáp án: A
Chia sẻ
About Toanbitexdtgd1
