BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Hàng điểm điều hòa và áp dụng (bài 2)
- 16/01/2023
- 96 lượt xem
| Ví dụ 2: Từ một điểm $A$ nằm ngoài đường tròn $(O)$ kẻ hai tiếp tuyến $AB$ và $AC$ đến $(O)$ (với $B,C$ là tiếp điểm). Kẻ cát tuyến $AEF$ không đi qua $O$ ($E$ nằm giữa $A$ và $F$). Đường thẳng qua $E$ và vuông góc với $OB$ cắt $BC$ tai $H$ và cắt $BF$ taị $K$. Chứng minh $HE = HK$. |
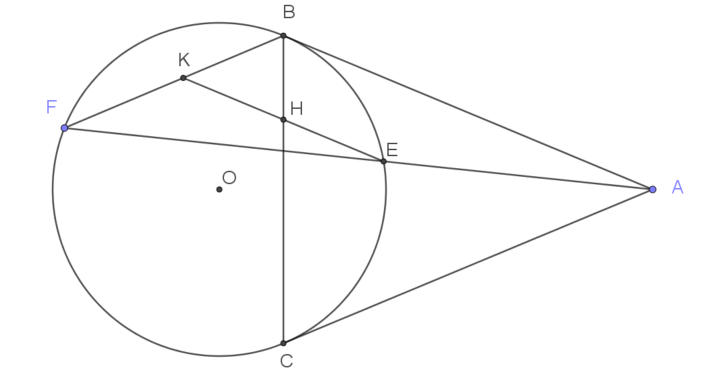
GIẢI
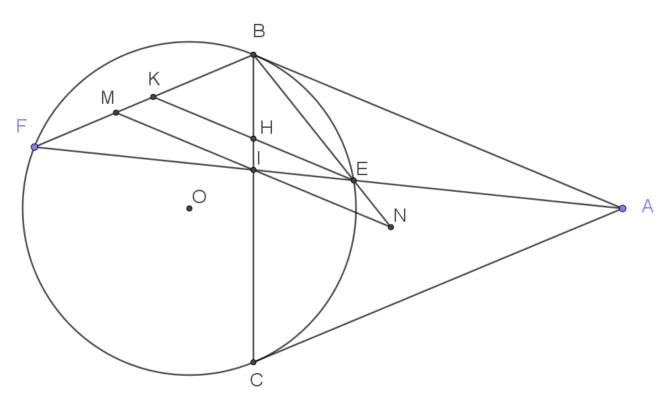
Ta có nhận xét: Đường thẳng vuông góc với $OB$ chính là đường thẳng song song với $AB$.
Gọi $I$ là giao điểm của $BC$ và $AF$. Từ $I$ ta vẽ đường thẳng song song với $AB$ cắt $BF$ và $BE$ lần lượt tại $M$ và $N$. Để chứng minh $H$ là trung điểm $KE$ ta chỉ cần chứng minh $I$ là trung điểm $MN$.
Ta có: $\dfrac{IM}{AB}=\dfrac{FI}{FA}\ ; \quad \dfrac{IN}{AB}=\dfrac{EI}{EA}; \quad \dfrac{FI}{FA}=\dfrac{EI}{EA}$ xem chứng minh ở bài 1
Vậy $IM=IN\Rightarrow HK=HE$.
Trở lại ví dụ 1 – hàng điểm điều hòa
Xem thêm Chứng minh trung điểm dựa vào tam giác đồng dạng
Xem thêm Chứng minh trung điểm dựa vào đường thẳng Steiner
Chia sẻ
About TS. Nguyễn Thái Sơn
