BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Chứng minh trung điểm dựa vào tam giác đồng dạng
- 16/01/2023
- 153 lượt xem
| Dựa vào tam giác đồng dạng ta tính được tỉ số đồng dạng. Từ tỉ số đồng dạng ta tính được một đoạn theo ba đoạn còn lại. Khi tính được hai đoạn cần chứng minh (là bằng nhau) ta chỉ cần so sánh các kết quả để suy ra hai đoạn đó bằng nhau. |
| Ví dụ 1: Cho điểm $M$ nằm ngoài đường tròn $(O)$. Qua $M$ kẻ hai tiếp tuyến $MA$, $MB$ VÀ cát tuyến $MCD$ $(A,B,C,D$ cùng thuộc đường tròn $(O)$), tia $MC$ nằm giữa tia $MO$ và $MA$. Vẽ đường kính $BE$ của đường tròn $(O)$. Từ $C$ vẽ đường thẳng song song với $OM$ cắt các đường thẳng $BE$ và $ED$ lần lượt tại $I$, $P$. Chứng minh $I$ là trung điểm $CP$. |
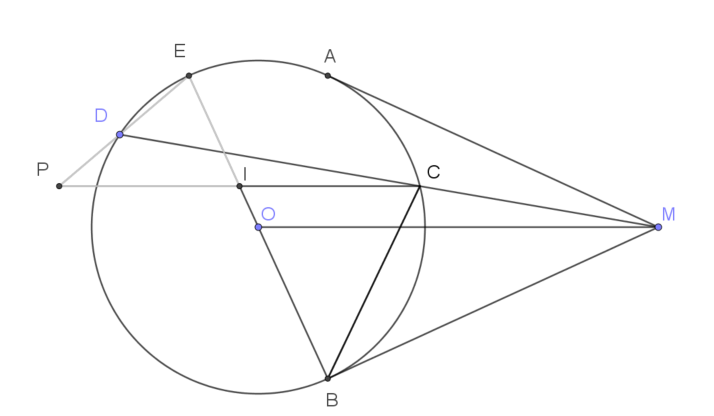
GIẢI
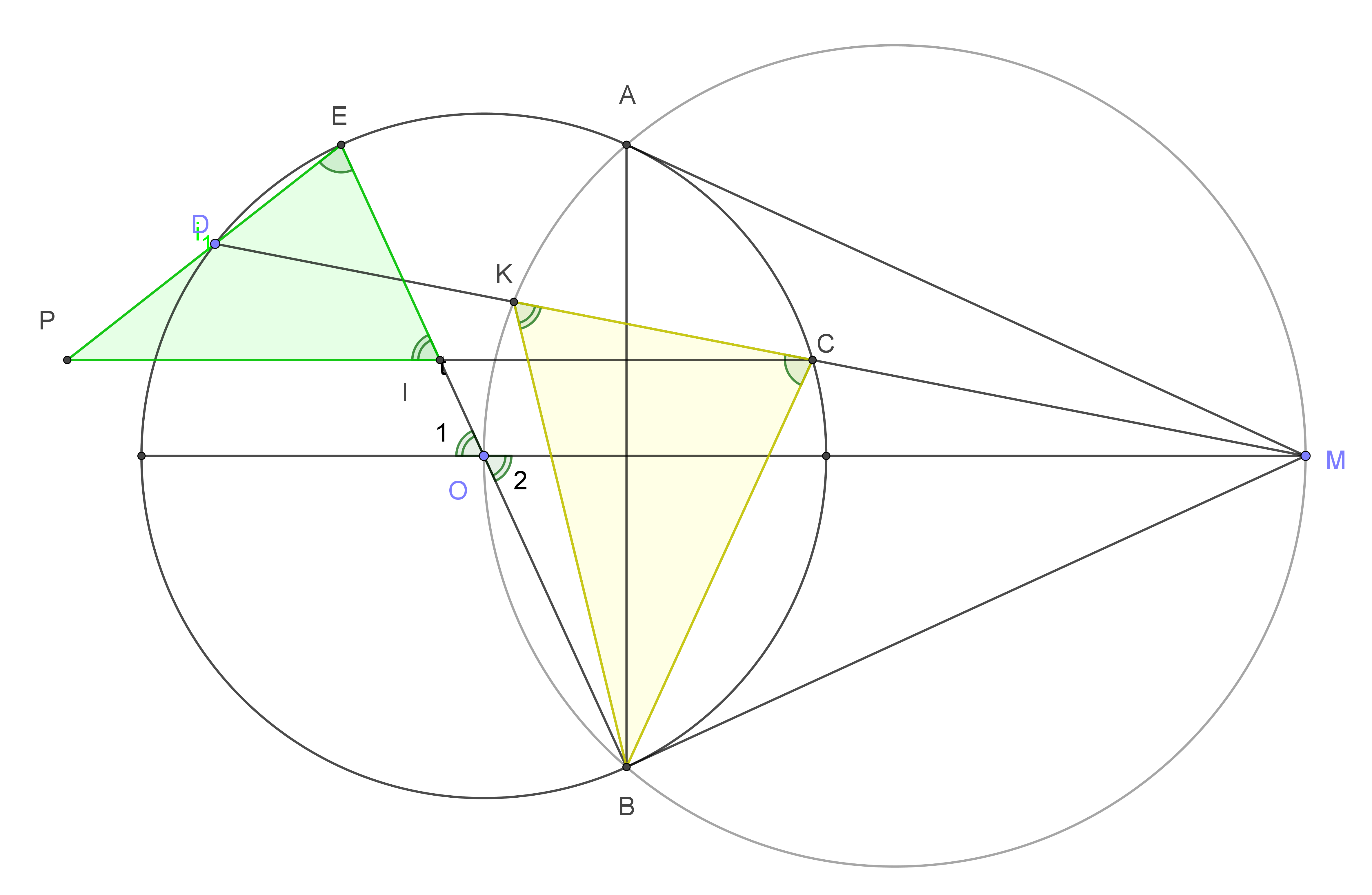
Xét hai tam giác $\triangle EIP$ và $\triangle CKB$ ta có:
$\widehat{IEP}=\widehat{KCB}$ (cùng chắn cung BD)
$\widehat{EIP}=\widehat{O_1}$ (đồng vị) $=\widehat{O_2}$ (đối đỉnh) $=\widehat{BKC}$ (cùng chắn cung BM). Suy ra $\widehat{EIP}=\widehat{BKC}$
Vậy $\triangle EIP \backsim \triangle CKB \Rightarrow IP=KB.\dfrac{EI}{KC}\quad (1)$.
Tương tự
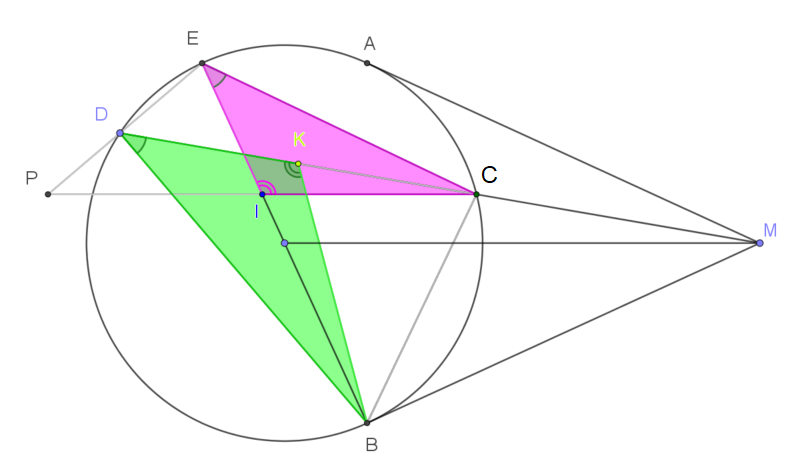
$\triangle EIC \backsim \triangle DKB \Rightarrow IC=IE.\dfrac{KB}{KD}\quad (2)$
Vì $KC=KD$ nên từ $(1)$ và $(2)$ ta suy ra $IP=IC$ (đpcm).
| Ví dụ 2: Từ một điểm $A$ nằm ngoài đường tròn $(O)$ kẻ hai tiếp tuyến $AB$ và $AC$ đến $(O)$ (với $B, C$ là tiếp điểm). Kẻ cát tuyến $AEF$ không đi qua $O$ ($E$ nằm giữa $A$ và $F$). Gọi $D$ là điểm đối xứng của $B$ qua $O$. Các tia $DE$ và $DF$ cắt $AO$ lần lượt tại $M$ và $N$. Chứng minh: $OM = ON$. |
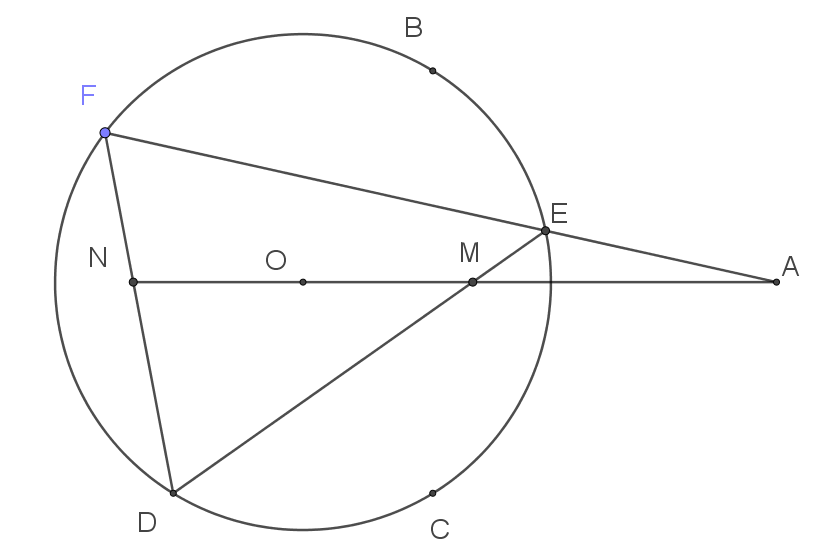
GIẢI
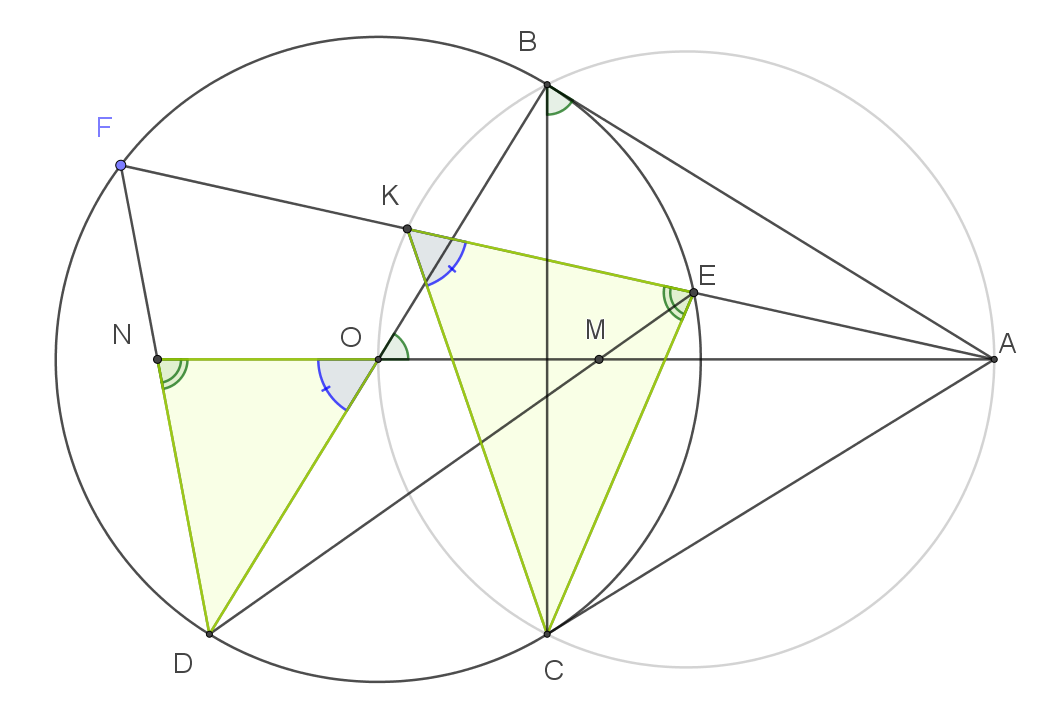
Gọi $K$ là trung điểm $EF$.
Xét hai tam giác $\triangle OND$ và $\triangle KEC$ ta có:
$\widehat{OND}=\widehat{KEC}\quad (1)$ (do $\triangle DMN \backsim \triangle CFE$) (việc chứng minh hai tam giác này đồng dạng dành cho bạn đọc.)
$\widehat{NOD}=\widehat{BOA}$ (đối đỉnh) $=\widehat{CBA}$ (cùng phụ với $\widehat{OBC}$) $=\widehat{CKE}$ (cùng chắn cung CA). Suy ra $\widehat{NOD}=\widehat{CKE}\quad (2)$.
Từ $(1)$ và $(2)$ suy ra $\triangle OND \backsim\triangle KEC\Rightarrow ON=KE.\dfrac{OD}{KC}\quad (3)$.
Chứng minh tương tự $\triangle OMD \backsim \triangle KFC \Rightarrow OM=KF.\dfrac{OD}{KC} \quad (4)$.
Vì $KE=KF$ nên từ $(3)$ và $(4)$ ta suy ra $ON=OM$ (đpcm).
Xem thêm Chứng minh trung điểm dựa vào chùm đường thẳng điều hòa
About TS. Nguyễn Thái Sơn
