Hàng điểm điều hòa và áp dụng
- 11/01/2023
- 243 lượt xem
| Trong các bài toán hình học lớp 9 có liên quan đến hai tiếp tuyến kẻ từ một điển nằm ngoài đường tròn, nhiều bài toán đề cập đến việc chứng minh một điểm trên đoạn thẳng nối hai tiếp điểm là trung điểm của một đoạn thẳng có phương song song với một trong hai tiếp tuyến. Việc chứng minh bài toán đó không dễ. Ở đây chúng tôi giới thiệu với một số em HSG lớp 9, quý vị phụ huynh và các thầy cô tìm hiểu thêm một khái niệm tuy sơ cấp nhưng rất hữu ích. |
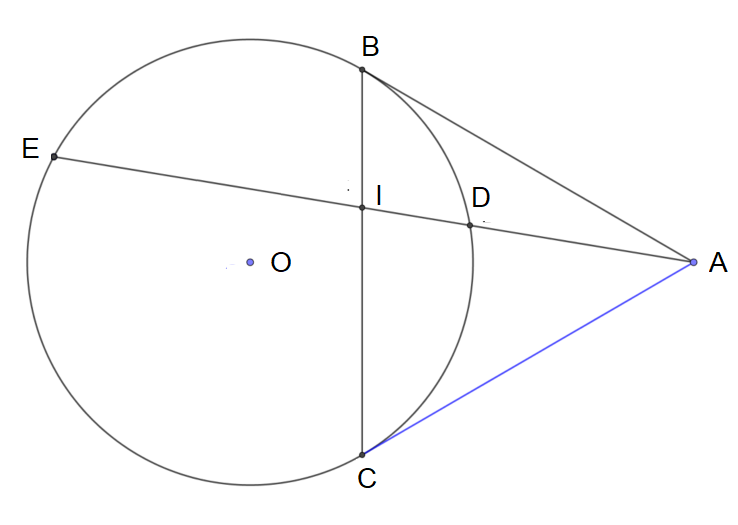
| Bài toán
Từ một điểm $A$ nằm ngoài đường tròn tâm $O$ ta vẽ hai tiếp tuyến $AB, AC$ (với $B$ và $C$ là hai tiếp điểm). Lấy một điểm $I$ tùy ý trên đoạn $BC$. Đường thẳng $AI$ cắt đường tròn tại cặp điểm $D, E$ (trong đó $D$ nằm giữa $A$ và $E$). Chứng minh rằng $$\dfrac{EI}{EA}=\dfrac{DI}{DA}$$ |
| Khi đó ta nói 4 điểm $I, A, E, D$ (theo đúng thứ tự đó) là một hàng điểm điều hòa. |
Chứng minh
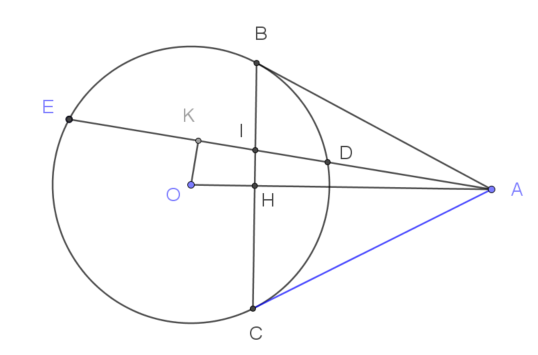
Gọi $K$ là trung điểm $DE$ và $H$ là giao điểm của $BC$ và $AO$. Tứ giác $OHIK$ nội tiếp đường tròn đường kính $OI$ nên:
$AI.AK=AH.AO=AB^2=AD.AE=(AK-KD)(AK+KD)=AK^2-KD^2$
Suy ra $(AK-KI).AK=AK^2-KD^2\Rightarrow KI.KA=KD^2$.
Bây giờ ta tính $\dfrac{EI}{EA}$.
Ta có:
$\dfrac{EI}{EA}=\dfrac{EK+KI}{EK+KA}=\dfrac{KD+\dfrac{KD^2}{KA}}{KD+KA}=\dfrac{KD}{KA}$
$\dfrac{DI}{DA}=\dfrac{DK-KI}{KA-KD}=\dfrac{KD-\dfrac{KD^2}{KA}}{KD-KA}=\dfrac{KD}{KA}$
Vậy $$\dfrac{EI}{EA}=\dfrac{DI}{DA}$$
| Lưu ý: Ngoài Phương pháp tính toán trực tiếp ở trên, at có thể sử dụng tính chất của đường phân giác trong và đường phân giác ngoài của một góc trong tam giác như sau:
Chứng minh $HI$ là đường phân giác trong góc $H$ của tam giác $EHD$, Vì $HA\perp HI$ nên $HA$ là đường phân giác ngoài góc $H$ của tam giác $EHD$. Theo tính chất của đường phân giác ta có: $\dfrac{IE}{ID}=\dfrac{AE}{AD} \quad \text{vì cùng bằng} \dfrac{HE}{HD}$ |
| Áp dụng:
Từ một điểm $A$ ở ngoài đường tròn $(O)$, kẻ hai tiếp tuyến $AB,AC (B,C$ là tiếp điểm) và cát tuyến $ADE$ đến đường tròn (tia $AE$ nằm trong góc $\widehat{OAB}$ và điểm $D$ nằm giữa $A$ và $E$). Gọi $I$ là giao điểm của $BC$ với $AE$. Qua $I$ kẻ đường thẳng song song với $AC$, cắt C$D$ và $CE$ lần lượt tại $M$ và $N$. Chứng minh $I$ là trung điểm của $MN$. |
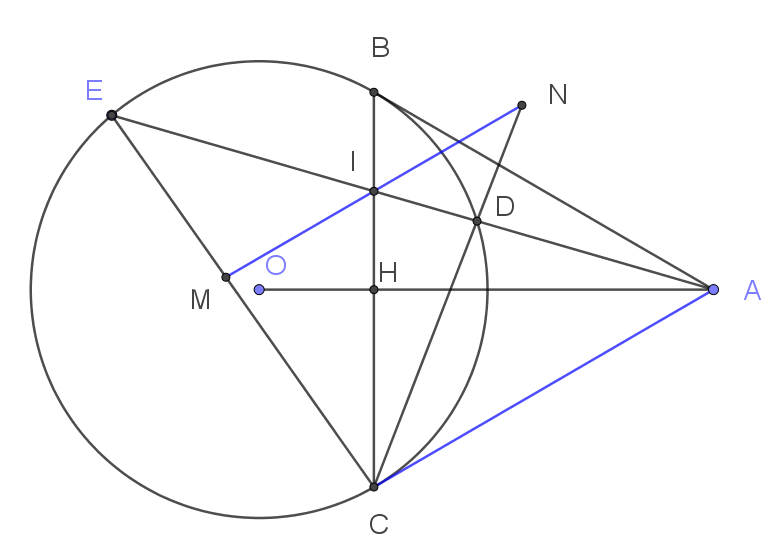
Áp dụng định lý Thales vào các tam giác $ECA$ và $DCA$ ta có:
$$\dfrac{IM}{CA}=\dfrac{EI}{EA} ;\quad ; \dfrac{IN}{CA}=\dfrac{DI}{DA}$$
Theo chứng minh trên $\dfrac{EI}{EA}=\dfrac{DI}{DA}$ do đó $IM=IN$ (đpcm).
| Lưu ý:
Do vị trí của các điểm trên đoạn thẳng $AE$ được sắp xếp theo một thứ tự thuận tiện nên việc phân tích thành tổng và hiệu là hoàn toàn hợp lý. Tính chất $I$ là trung điểm của đoạn thẳng $MN$ là một tính chất đặc trưng của chùm đường thẳng điều hòa. Ở đây ta chứng minh trực tiếp như một áp dụng của tứ giác nội tiếp thuộc chương trình lớp 9. |
Xem tiếp Hàng điểm điều hòa – Bài 2
Xem thêm Chứng minh trung điểm dựa vào tam giác đồng dạng
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay