Chứng minh trung điểm dựa vào đường thẳng Steiner
- 28/01/2023
- 261 lượt xem
| 1. Đường thẳng Simson |
Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $M$ là một điểm tùy ý trên đường tròn. Goi $D, E, F$ lần lượt là hình chiếu vuông góc của $M$ trên ba cạnh $BC, CA, AB$ của tam giác. Chứng minh 3 điểm $D, E, F$ thẳng hàng trên một đường thẳng mà ta gọi là đường thẳng Simson.
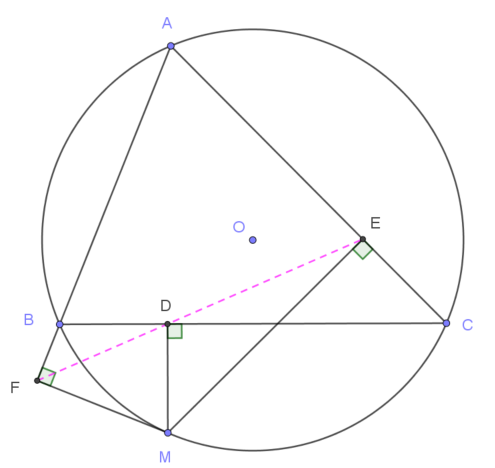
Chứng minh
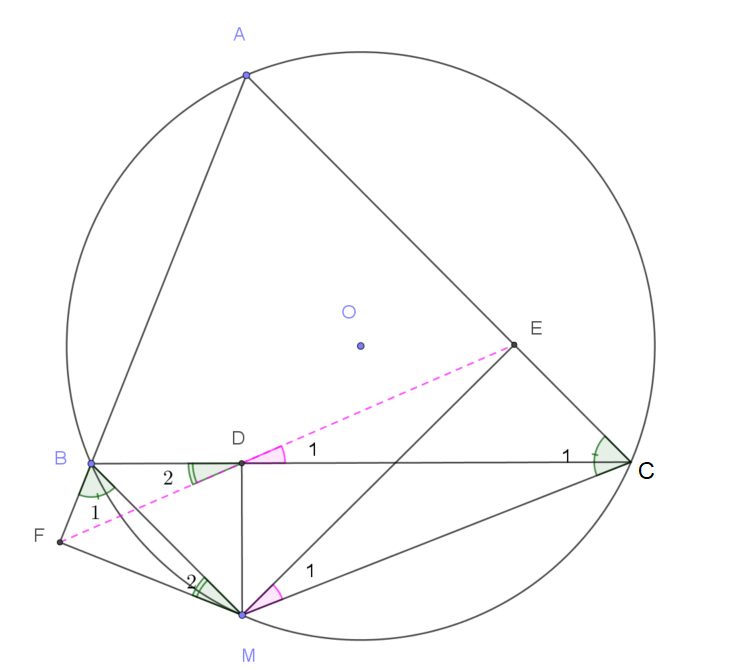
Ta có: $\widehat{D_1}=\widehat{M_1}$ (cùng chắn cung $EC$ vì tứ giác $MDEC$ nội ttếp đường tròn đường kính $MC$).
$\widehat{M_1}=90^\circ -\widehat{MCA}$ nên $\widehat{D_1}=90^\circ -\widehat{MCA}\quad (1)$.
Tương tự $\widehat{D_2}=90^\circ -\widehat{MBF}\quad (2)$
Tứ giác $ABMC$ nội tiếp nên $\widehat{MCA}=\widehat{MBF}\quad (3)$.
Từ (1), (2) và (3) ta suy ra $\widehat{D_1}=\widehat{D_2}$ suy ra ba điểm $D, E, F$ thẳng hàng.
| 2. Đường thẳng Steiner |
Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $M$ là một điểm tùy ý trên đường tròn. Goi $D’, E’, F’$ lần lượt là điểm đối xứng của $M$ qua ba cạnh $BC, CA, AB$ của tam giác. Chứng minh 3 điểm $D’, E’, F’$ thẳng hàng trên một đường thẳng mà ta gọi là đường thẳng Steiner.
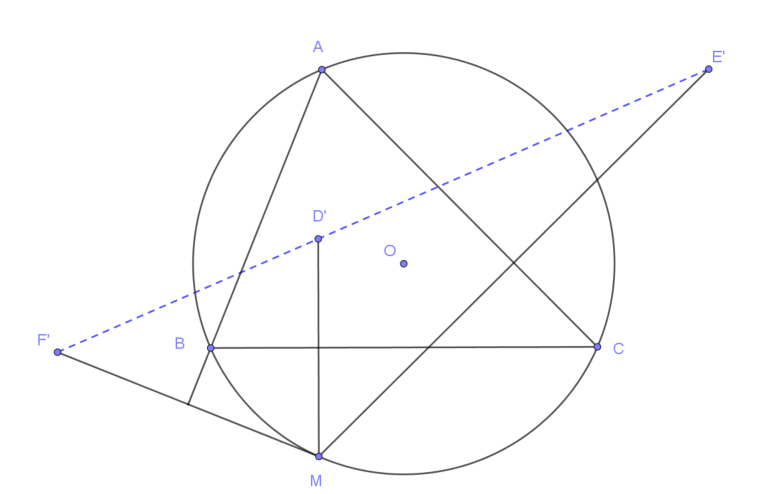
Chứng minh
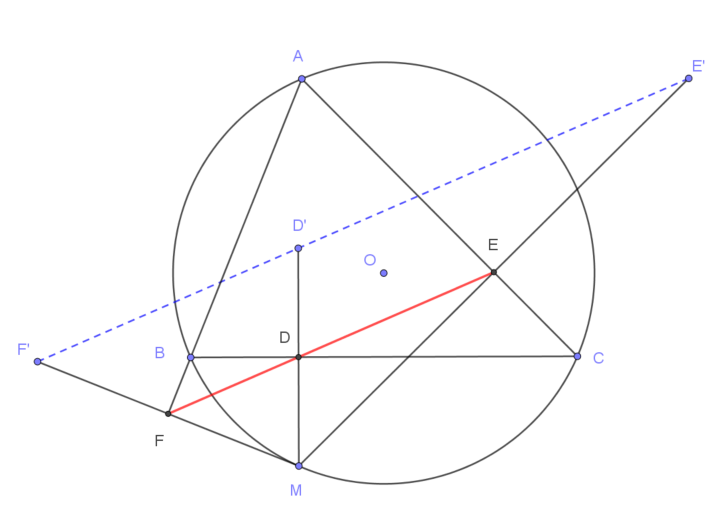
Gọi $D, E, F$ lần lượt là hình chiếu vuông góc của $M$ trên ba cạnh $BC, CA, AB$ của tam giác. Khi đó $D, E, F$ cũng lần lượt là trumg điểm của các đoạn thẳng $MD’, ME’, MF’$ và 3 điểm $D, E, F$ thẳng hàng trêm đường thẳng Simson.
Theo định lý đường trung bình ta có:$$F’D’/\!/FD\ ,\ D’E’/\!/DE$$
Vì $D, E, F$ thẳng hàng nên $D’, E’, F’$ thẳng hàng.
| 3. Áp dụng |
Cho $\triangle ABC$ nhọn $(AB < AC)$ nội tiếp đường tròn tâm $O$. Điểm $M$ thuộc cung nhỏ $BC$. Vẽ $ME,MF$ lần lượt vuông góc $AC,AB$ tại $E, F$.Gọi $H$ là trực tâm của $\triangle ABC$, đường thẳng $EF$ cắt $HM$ tại $I$. Chứng minh $I$ là trung điểm $HM$.
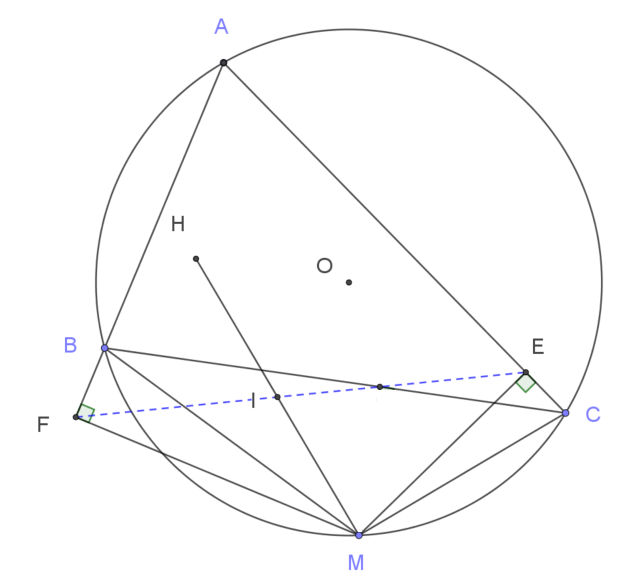
Chứng minh
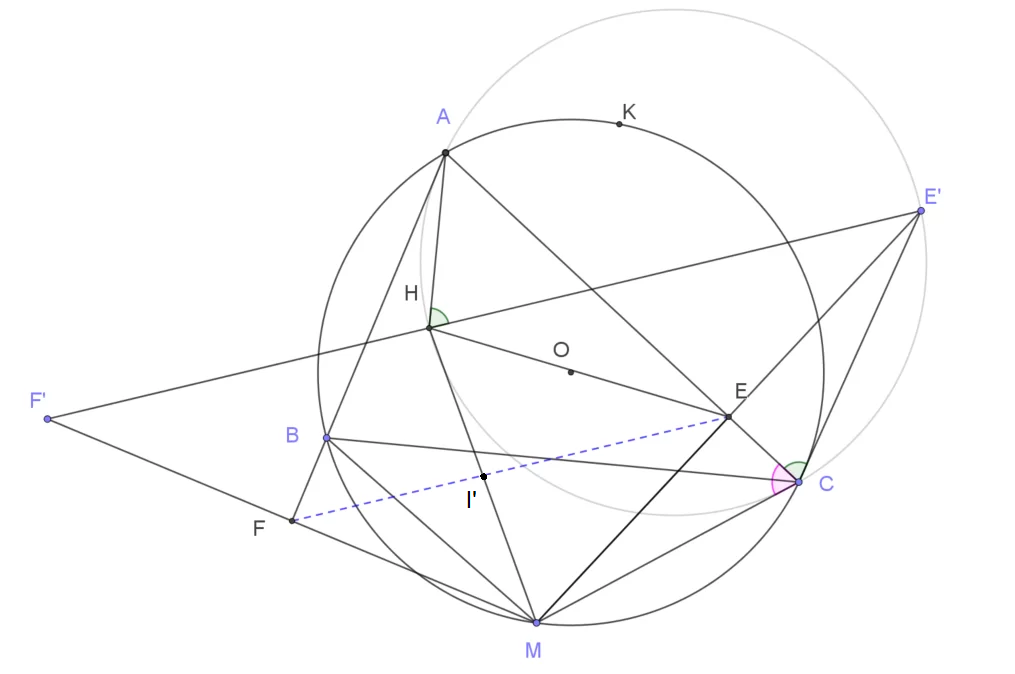
Gọi $K$ là điểm đối xứng của $H$ qua $AC$. Khi đó $K$ nằm trên đường tròn $(O)$ (độc giả tự chứng minh điều này: đối xứng của trực tâm qua một cạnh thì nằm trên đường tròn ngoại tiếp).
Gọi $E’, F’$ lần lượt là điểm đối xứng của $M$ qua các cạnh $AC$ và $AB$. Khi đó đường thẳng $E’F’$ là đường thẳng Steiner ứng với điểm $M$.
Ta chứng minh tứ giác $AHCE’$ nội tiếp. Thật vậy, $\widehat{AE’H}=\widehat{AMK}$ (chú ý sự đối xứng.)
$\widehat{AMK}=\widehat{ACK}$ (cùng chắn cung $AK$)
$\widehat{ACK}=\widehat{ACH}$ (chú ý sự đối xứng.)
Vậy $\widehat{AE’H}=\widehat{ACH}$ (đpcm).
Vì tứ giác nói trên nội tiếp nên $\widehat{AHE’}=\widehat{ACE’}=\widehat{ACM}$.
Hoàn toàn tương tự $\widehat{AHF’}=\widehat{ABF’}=\widehat{ABM}$
Vậy $\widehat{AHE’}+\widehat{AHF’}=\widehat{ACM}+\widehat{ABM}=180^\circ$. Suy ra $H$ nằm trên đường thẳng $E’F’$.
Bây giờ ta gọi $I’$ là trung điểm $HM$ . Khi đó $$I’F/\!/HF’\ , \ I’E/\!/HE’$$
Vì $F’, H, E’$ thẳng hàng nên $F, I’,E$ thẳng hàng, nghĩa là $I’$ là giao điểm của hai đường thẳng $FE$ và $HM$, do đó $I’\equiv I$. Kết luận $I$ là trung điểm $HM$.
| Lưu ý: Trung điểm $I$ của $HM$ còn một tính chất thú vị nửa, đó là nó nằm trên đường tròn Euler của tam giác $ABC$, tức là đường tròn đi qua trung điểm của ba đoạn thẳng $HA, HB, HC$. |
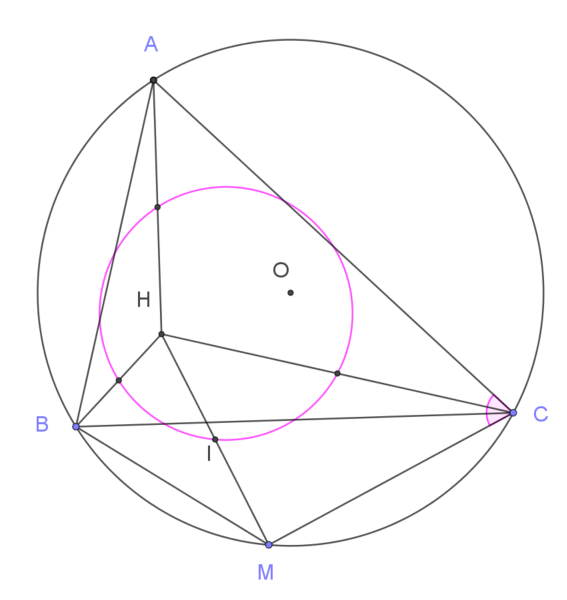
Việc chứng minh dành cho bạn đọc. Về phương diện hình học lớp 11, đường tròn Euler là ảnh của đường tròn ngoại tiếp qua phép vị tự tâm $H$ tỉ số vị tự là $\dfrac12$ (giống như việc photocopy thu nhỏ). Đối với hình học lớp 9 ta chứng minh tứ giác nội tiếp.
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay