Một bài MOD 2015^2015 khá hóc búa!

Đề bài: Tìm dư khi chia

$A=1^{2015}+2^{2015}+...+2015^{2015}$ cho 11.

(Trả lời cho thành viên quanghieu trên Facebook Diễn đàn)

Bài giải:

Ta chia thành các nhóm sau để tìm dư:

+Nhóm 1: Các số từ 1 tới 11, nhưng vì $11^{2015}\vdots 11$ nên thực chất ta chỉ xét từ 1 tới 10.

+Nhóm 2: Các số từ 12 tới 22, và cũng tương tự ta chỉ xét tới 21.

…

Số nhóm cần tách là 2015Qa11= = 183 nhóm.

Mặt khác ta có công thức sau: $\left ( a+b \right )^{n}\equiv b^{n}\left ( moda \right )\left ( a>0 \right )$

Ta đi tính dư:

8 11

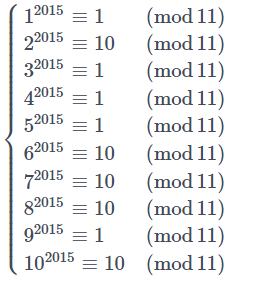
Vậy

$A=1^{2015}+2^{2015}+...+2015^{2015}$

$\Leftrightarrow A\equiv \left ( 1\times 5 \right+10\times 5 )$ . $\frac{2013}{11}$ $+2014^{2015}+2015^{2015}$

$\Leftrightarrow A\equiv 55\times 183+1+10$

$\Leftrightarrow A\equiv 0(mod11)$

Chia sẻ

BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay