BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
ỨNG DỤNG TÍCH PHÂN VÀO MỘT SỐ BÀI TOÁN VẬN TỐC
- 20/12/2018
- 28,068 lượt xem
Các bài toán thực tế trong đề thi THPT Quốc Gia thường gây khó khăn cho các thí sinh. Do đó, Diễn đàn máy tính cầm tay muốn giới thiệu đến bạn đọc một vài ví dụ cơ bản về ứng dụng tích phân vào bài toán thực tế liên quan đến kiến thức vật lý.
Xem thêm: ỨNG DỤNG TÍCH PHÂN GIẢI NHANH CÁC BÀI TOÁN THỰC TẾ VỀ TÍNH DIỆN TÍCH
Ví dụ 1: Vận tốc chuyển động của máy bay là $latex v(t)=6{{t}^{2}}+1(m/s)$. Hỏi quãng đường máy bay bay từ giây thứ 5 đến giây thứ 15 là bao nhiêu?
A. $latex 2400m$ B. $latex 1202m$ C. $latex 6510m$ D. $latex 1134m$
Hướng dẫn giải:
Quãng đường đi được $latex S(t)$ là nguyên hàm của vận tốc $latex v(t)$. Do đó quãng đường đi được từ giây thứ 5 đến giây thứ 15 là:
$latex S=\int\limits_{5}^{15}{v(t)dt=\int\limits_{5}^{15}{\left( 6{{t}^{2}}+1 \right)dt}}$
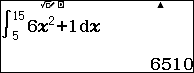
Đáp án C
Ví dụ 2: (SGK- Toán 12 NC)
Một xe ô tô đang chạy thì phanh lại. Sau khi đạp phanh, ô tô bắt đầu chuyển động chậm dần đều với vận tốc $latex v(t)=-40t+20(m/s)$, trong đó $latex t$ là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét ?
A. $latex 4.5(m)$ D. $latex 5(m)$ C. $latex 5.5(m)$ D. $latex 6(m)$
Hướng dẫn giải
Chọn mốc thời gian là lúc người lái xe đạp phanh và $latex T$ là thời điểm ô tô dừng hẳn
Khi đó $latex v(T)=0$ hay $latex -40T+20=0$. Suy ra $latex T=0.5$
Như vậy, kể từ lúc đạp phanh ô tô mất thêm $latex 0.5s$ để dừng hẳn và quãng đường ô tô di chuyển trong thời gian này là:
$latex S=\int\limits_{0}^{0.5}{v(t)dt=}\int\limits_{0}^{0.5}{(-40t+20)dt}$
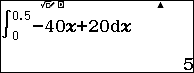
Đáp án: B
Ví dụ 3: (Đề THPT Quốc Gia 2018)
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian quy luật $latex v(t)=\dfrac{1}{120}{{t}^{2}}+\dfrac{58}{45}t(m/s)$ trong đó $latex t$ (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 3 giây so với và có gia tốc bằng $latex a(m/{{s}^{2}})$ ($latex a$ là hằng số). Sau khi B xuất phát được $latex 15s$ thì đuổi kịp A. Vận tốc B tại thời điểm đuổi kịp A bằng
A. $latex 25(m/s)$ B. $latex 30(m/s)$ C. $latex 36(m/s)$ D. $latex 21(m/s)$
Hướng dẫn giải
- Tính quãng đường A đi được cho đến khi B đuổi kịp A
$latex S=\int\limits_{5}^{15}{v(t)dt=\int\limits_{5}^{15}{\left( 6{{t}^{2}}+1 \right)dt}}$
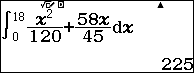
- Tính quãng đường B đi được cho đến khi B đuổi kịp A
Vận tốc của B tại thời điểm $latex t(s)$ tính từ lúc B xuất phát là $latex {{v}_{B}}(t)=at(m/s)$
Quãng đường B đi được cho đến khi B đuổi kịp A
$latex S=\int\limits_{0}^{15}{{{v}_{B}}(t)dt=\int\limits_{0}^{15}{at}}dt=\dfrac{a{{t}^{2}}}{2}\left| \begin{align} & 15 \\& 0 \\ \end{align} \right.=\dfrac{225}{2}a(m)$
- Tính vận tốc B tại thời điểm đuổi kịp A
$latex \dfrac{225}{2}a=225\Rightarrow a=2$
$latex {{v}_{B}}(t)=2t\Rightarrow {{v}_{B}}(15)=30(m/s)$
Đáp án B
Lưu ý:
Để có thể làm tốt các bài toán trên, chúng ta cần nhớ mối hệ của các đại lượng Quãng đường $latex S\left( t \right)$ , Vận tốc $latex v\left( t \right)$ và Gia tốc $latex a\left( t \right)$
- Quãng đường đi được $latex S\left( t \right)$là nguyên hàm của vận tốc $latex v\left( t \right)$
- Quãng đường đi được của vật trong khoảng thời gian nào bằng tích phân của hàm vận tốc $latex v\left( t \right)$ khi biến $latex t$ chạy trong khoảng thời gian đó.
- Đạo hàm của vận tốc $latex v\left( t \right)$ tại thời điểm $latex t$ chính là gia tốc của vật chuyển động tại thời điểm đó $latex a\left( t \right)$ .
————————————-
Cảm ơn các bạn đã theo dõi bài viết ỨNG DỤNG TÍCH PHÂN VÀO MỘT SỐ BÀI TOÁN VẬN TỐC trên. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
keywords: tích phân, ứng dụng tích phân
About Ngọc Hiền Bitex
