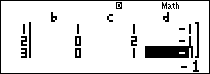BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Ứng Dụng Hệ Phương Trình Bậc Nhất 3 Ẩn Viết Phương Trình Mặt Phẳng Đi Qua Ba Điểm
- 22/12/2017
- 1,917 lượt xem
Trong không gian với hệ toạ độ Oxyz, cho các điểm [latex]A\left( { – 1;1;1} \right)[/latex] ,[latex]B\left( { 3;0;2} \right)[/latex] và [latex]C\left( { 1;0;1} \right)[/latex]. Phương trình mặt phẳng (P) đi qua ba điểm A,B,C là:
A). [latex]\left( P \right):x – 2y – 2{\text{z}} + 5 = 0[/latex]
B). [latex]\left( P \right):x – 2y + 2{\text{z}} + 5 = 0[/latex]
C). [latex]\left( P \right):x – 2y + 2{\text{z}} + 3 = 0[/latex]
D). [latex]\left( P \right):x – 2y – 2{\text{z}} + 1 = 0[/latex]
Giải.
Ta sẽ nhập phương trình bậc nhất 3 ẩn số theo tọa độ của ba điểm với [latex]a = x;b = y;c = z;d = – 1[/latex] mặt định cho [latex]d= – 1[/latex] ta có được hệ phương trình sau.
[latex]\left\{ \begin{gathered} – x + y + z = – 1 \hfill \\ 3x + 0y + 2z = – 1 \hfill \\ x + 0y + z = – 1 \hfill \\ \end{gathered} \right.[/latex]Nhập vào màn hình máy tính.
Vậy ta được [latex]x = 1;y = 2,z = – 2 \Rightarrow \overrightarrow n = (1;2; – 2)[/latex]
Vậy phương trình của mặt (P) có dạng [latex]x + 2y – 2z + D = 0[/latex] và (P) qua [latex]A( – 1;1;1) \Rightarrow D = 1[/latex]
Vậy (P) có phương trình là: [latex]\left( P \right):x – 2y – 2{\text{z}} + 1 = 0[/latex]
About toancasiobitex
