BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Sử dụng hệ phương trình để giải quyết một số bài toán trong đề thi minh họa THPT 2019
- 23/12/2018
- 1,409 lượt xem
Trong bài viết này, Diễn đàn máy tính cầm tay sẽ trình bày cách giải quyết 2 bài toán vận dụng cao trong đề thi minh họa THPT Quốc gia 2019 bằng phương pháp lập hệ phương trình nhằm xác định được hàm số thõa mãn đề bài.
Bài 1 (câu 43- Đề thi tham khảo THPT 2019)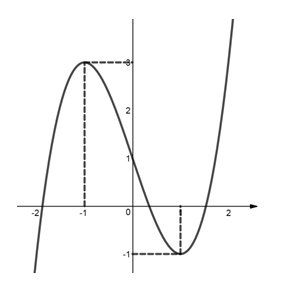
Cho hàm số $latex y=f\left( x \right)$ liên tục trên $latex \mathbb{R}$ và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số $latex m$ để phương trình $latex f\left( \operatorname{s}\text{inx} \right)=m$ có nghiệm thuộc khoảng $latex \left( 0;\pi \right)$ là
- $latex \left[ -1;3 \right)$
- $latex \left( -1;1 \right)$
- $latex \left( -1;3 \right)$
- $latex \left[ -1;1 \right)$
Hướng dẫn giải
Cách 1: Biện luận
Đặt $latex t=\operatorname{s}\text{inx}$
Dựa vào đường tròn lượng giác ta xác định được khoảng giá trị của $latex t$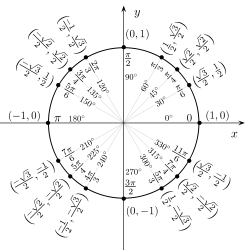
Với $latex x\in \left( 0;\pi \right)$ thì $latex t\in \left( 0;1 \right]$
Khi đó phương trình $latex f\left( \operatorname{s}\text{inx} \right)=m$ trở thành $latex f\left( t \right)=m$ với $latex t\in \left( 0;1 \right]$
Như vậy nghiệm của phương trình $latex f\left( t \right)=m$ là giao điểm của đồ thị hàm số $latex y=f\left( t \right)$ và đường thẳng $latex y=m$
Dựa vào đồ thị ta thấy để $latex f\left( t \right)=m$ có nghiệm $latex t\in \left( 0;1 \right]$ thì $latex m\in \left[ -1;1 \right)$
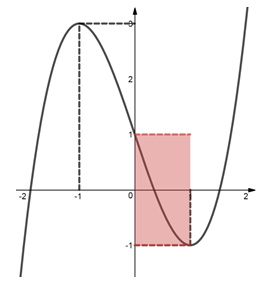
Cách 2: Sử dụng máy tính cầm tay tìm hàm số $latex f\left( x \right)$
Quan sát hình vẽ nhận thấy hàm số của đồ thị trong đề thi tham khảo có dạng bậc 3 $latex \left( C \right):f\left( x \right)={{x}^{3}}+a{{x}^{2}}+bx+c$
$latex \left( C \right)$ đi qua các điểm $latex \left( -1;3 \right);\left( 0;1 \right)$ và $latex \left( 1;-1 \right)$. Do đó ta có thể sử dụng Casio fx 580vnx giải hệ phương trình:
$latex \left\{ \begin{align} & a-b+c=4 \\ & c=1 \\ & a+b+c=-2 \\\end{align} \right.$$latex \Leftrightarrow \left\{ \begin{align} & a=0 \\ & b=-3 \\ & c=1 \\\end{align} \right.$
Như vậy hàm số của đồ thị trong đề thi tham khảo này là $latex \left( C \right):f\left( x \right)={{x}^{3}}-3x+1$
Suy ra: $latex f\left( \operatorname{s}\text{inx} \right)={{\sin }^{3}}x-3\sin x+1=m$
Dựa theo đáp án của đề bài ta thử $latex m=-1$
Dùng Casio fx 580vnx giải phương trình $latex {{\sin }^{3}}x-3\sin x+1=-1\Leftrightarrow \left[ \begin{align} & \sin x=-2\left( L \right) \\ & \sin x=1\Rightarrow x=\dfrac{\pi }{2}\left( N \right) \\\end{align} \right.$
Suy ra: $latex m=-1$ thõa bài toán. Như vậy ta loại được B và C
Tiếp tục thử $latex m=1$
Tương tự dùng Casio fx 580vnx giải phương trình $latex {{\sin }^{3}}x-3\sin x+1=1\Leftrightarrow \left[ \begin{align} & \operatorname{s}\text{inx}=0\Rightarrow x=0\left( L \right) \\ & x=\pm \sqrt{3}\left( L \right) \\\end{align} \right.$
Suy ra $latex m=1$ không thõa bài toán. Như vậy ta loại được A và chọn D
Bài 2 (Câu 50- Đề thi tham khảo 2019)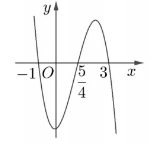
Cho hàm số $latex f\left( x \right)=m{{x}^{4}}+n{{x}^{3}}+p{{x}^{2}}+qx+r$$latex \left( m,n,p,q,r\in \mathbb{R} \right)$. Hàm số $latex y={f}’\left( x \right)$ có đồ thị như hình vẽ bên. Tập nghiệm của phương trình $latex f\left( x \right)=r$ có số phần tử
- $latex 4$
- $latex 3$
- $latex 1$
- $latex 2$
Hướng dẫn giải
Ta có:
$latex f\left( x \right)=m{{x}^{4}}+n{{x}^{3}}+p{{x}^{2}}+qx+r$
$latex \Rightarrow {f}’\left( x \right)=4m{{x}^{3}}+3n{{x}^{2}}+2px+q=m\left( 4{{x}^{3}}+\dfrac{3n}{m}{{x}^{2}}+\dfrac{2p}{m}x+\dfrac{q}{m} \right)$
$latex \Rightarrow \dfrac{{f}’\left( x \right)}{m}=4{{x}^{3}}+\dfrac{3n}{m}{{x}^{2}}+\dfrac{2p}{m}x+\dfrac{q}{m}$
Đồ thị hàm số $latex y={f}’\left( x \right)$ cắt trục Ox tại 3 điểm $latex \left( -1;0 \right)$ ;$latex \left( \dfrac{5}{4};0 \right)$ và $latex \left( 3;0 \right)$. Do đó ta có hệ phương trình
$latex \left\{ \begin{matrix} 3a & – & 2b & + & c & = & 4 \\ 3{{\left( \dfrac{5}{4} \right)}^{2}}a & + & \dfrac{5}{2}b & + & c & = & -4{{\left( \dfrac{5}{4} \right)}^{3}} \\ 27a & + & 6b & + & c & = & -108 \\ \end{matrix} \right.$
Sử dụng máy tính Casio fx 580vnx giải hệ phương trình trên ta được:
$latex a=\dfrac{n}{m}=\dfrac{-13}{3}$ ; $latex b=\dfrac{p}{m}=-1$ và $latex c=\dfrac{q}{m}=15$
Giải phương trình $latex f\left( x \right)=r$
$latex m{{x}^{4}}+n{{x}^{3}}+p{{x}^{2}}+qx+r=r$
$latex \Leftrightarrow m{{x}^{4}}+n{{x}^{3}}+p{{x}^{2}}+qx=0$
$latex \Leftrightarrow {{x}^{4}}+\dfrac{n}{m}{{x}^{3}}+\dfrac{p}{m}{{x}^{2}}+\dfrac{q}{m}x=0$
$latex \Leftrightarrow {{x}^{4}}-\dfrac{13}{3}{{x}^{3}}-{{x}^{2}}+15x=0$
Sử dụng Casio fx 580vnx ta tìm nghiệm của phương trình trên:
$latex x=3;x=0$ và $latex x=\dfrac{-5}{3}$
Cảm ơn các bạn đã theo dõi bài viết SỬ DỤNG HỆ PHƯƠNG TRÌNH ĐỂ GIẢI QUYẾT MỘT SỐ BÀI TOÁN TRONG ĐỀ THI MINH HỌA THPT 2019 của chúng tôi. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
