BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
DÙNG CASIO fx 580vnx GIẢI QUYẾT CÁC BÀI TÍCH PHÂN HAY TRONG ĐỀ THI THAM KHẢO 2019
- 22/12/2018
- 2,261 lượt xem
Tích phân là một trong những chuyên đề hay và thường xuất hiện trong đề thi THPT Quốc gia từ những câu hỏi ở mức độ nhận biết đến các bài toán vận dụng.
Vì vậy, trong bài viết lần này Diễn đàn máy tính cầm tay sẽ giới thiệu đến bạn đọc các cách giải cho 2 bài toán tích phân hay trong đề thi tham khảo THPT Quốc gia 2019 dưới sự hỗ trợ của máy tính Casio fx 580vnx.
Bài 1: (Câu 38) Cho $latex \int\limits_{0}^{1}{\dfrac{xdx}{{{\left( x+2 \right)}^{2}}}}=a+b\ln 2+c\ln 3$ với $latex a,b,c$ là các số hữu tỷ. Giá trị của $latex 3a+b+c$ bằng
A. $latex -2$ B. $latex -1$ C. $latex 2$ D. $latex 1$
Hướng dẫn giải:
Cách 1: Khai triển công thức
Khai triển và tính tích phân $latex \int\limits_{0}^{1}{\dfrac{xdx}{{{\left( x+2 \right)}^{2}}}}$
Đặt $latex t=x+2\Rightarrow x=t-2\Rightarrow dt=dx$
Thay cận: $latex \begin{align} & x=0\Rightarrow t=2 \\ & x=1\Rightarrow t=3 \\ \end{align}$
Khi đó ta có: \[\int\limits_{0}^{1}{\dfrac{xdx}{{{\left( x+2 \right)}^{2}}}}=\int\limits_{2}^{3}{\dfrac{(t-2)dt}{{{t}^{2}}}}=\int\limits_{2}^{3}{\dfrac{dt}{t}}-2\int\limits_{2}^{3}{\dfrac{dt}{{{t}^{2}}}}=\ln t\left| _{2}^{3} \right.+2\left( \dfrac{1}{t} \right)\left| _{2}^{3}=\ln 3-\ln 2+\dfrac{1}{3} \right.\]
Suy ra: $latex a=\dfrac{-1}{3};b=-1;c=1$
Vậy: $latex 3a+b+c=-1$
Cách 2: Sử dụng máy tính Casio fx 580vnx
Sử dụng Casio fx 580vnx tính tích phân $latex \int\limits_{0}^{1}{\dfrac{xdx}{{{\left( x+2 \right)}^{2}}}}$ và gán vào A
Khi đó ta có $latex A=a+b\ln 2+c\ln 3\Leftrightarrow A-a=b\ln 2+c\ln 3\Rightarrow {{e}^{A-a}}={{2}^{b}}{{3}^{c}}$
Nhận xét: Quan sát đề ta thấy các đáp án đều là số nguyên nên $latex b,c$ có thể là số nguyên và $latex a$ là phân số có mẫu lược giản được với 3 nên ta sử dụng chức năng Table trong Casio fx 580vnx để tìm đáp án thích hợp
Nhập $latex f(x)={{e}^{A-x}}$, Bắt đầu: $latex -2$ , Kết thúc $latex -2$ và Bước: $latex \dfrac{1}{3}$
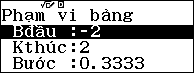
Quan sát bảng giá trị ta thấy tại $latex x=\dfrac{-1}{3}$ thì $latex f(x)=\dfrac{3}{2}$ (một phân số đơn giản)
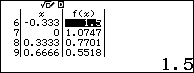
Như vậy ta có $latex a=\dfrac{-1}{3}$, $latex {{2}^{b}}{{3}^{c}}=\dfrac{3}{2}\Rightarrow b=-1;c=1$
Vậy: $latex 3a+b+c=-1$
Đáp án B
Bình luận:
Với bài toán trên chúng tôi đưa ra 2 hướng giải nhằm giúp bạn đọc có nhiều lựa chọn hơn khi làm bài. Mỗi phương pháp đều có những ưu nhược điểm nhất định. Cách 1 sẽ phù hợp hơn nếu bài toán tích phân đơn giản và thí sinh nắm vững các phương pháp khai triển tích phân. Tuy nhiên, khi gặp phải những bài toán tích phân phức tạp và thời lượng làm bài ít thì Cách 2 (Sử dụng máy tính Casio fx 580vnx) sẽ là lựa chọn hợp lý hơn.
Bài 2 (Câu 46): Một biển quảng cáo có dạnh hình elip với bốn đỉnh $latex {{A}_{1}},{{A}_{2}},{{B}_{1}},{{B}_{2}}$ như hình vẽ. Biết chi phí để sơn phần tô đậm là $latex 200.000$ đồng$latex /{{m}^{2}}$ và phần còn lại là $latex 100.000$ đồng$latex /{{m}^{2}}$ . Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết $latex {{A}_{1}}{{A}_{2}}=8m$,$latex {{B}_{1}}{{B}_{2}}=6m$ và tứ giác MNPQ là hình chữ nhật có$latex MQ=3m$
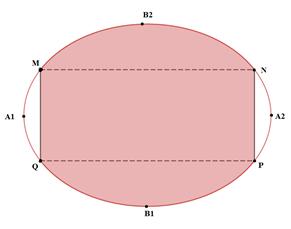A. $latex 7.322.000$ đồng B. $latex 7.213.000$ đồng C. $latex 5.526.000$ đồng D. $latex 5.782.000$ đồng
Hướng dẫn giải:
Gắn trục tọa độ $latex Oxy$ vào hình trên như sau:
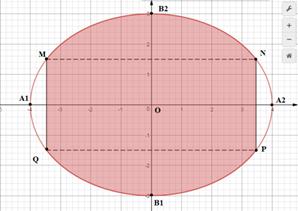
Ta có phương trình Elip có dạng tổng quát là $latex \left( E \right):\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ (với $latex a,b$ lần lượt là độ dài nữa trục ngang và nữa trục đứng của Elip)
Theo giả thiết ta có: $latex a=\dfrac{{{A}_{1}}{{A}_{2}}}{2}=4$ ; $latex b=\dfrac{{{B}_{1}}{{B}_{2}}}{2}=3$. Suy ra phương trình Elip là $latex \left( E \right):\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$
Vì $latex N\left( {{x}_{N}},1.5 \right)\in \left( E \right)$ nên $latex \dfrac{{{x}_{N}}^{2}}{16}+\dfrac{{{1.5}^{2}}}{9}=1\Rightarrow {{x}_{N}}=2\sqrt{3}$
- Sử dụng tích phân để tính diện tích các mặt phẳng:
Ta có: $latex \dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\Rightarrow y=\pm 3\sqrt{1-\dfrac{{{x}^{2}}}{16}}$
- Tính diện tích toàn bộ mặt phẳng Elip $latex {{S}_{\left( E \right)}}$
Do hình Elip đối xứng với nhau qua trục $latex \text{Ox}$ nên $latex {{S}_{(E)}}=2\int\limits_{-4}^{4}{\left( 3\sqrt{1-\dfrac{{{x}^{2}}}{16}} \right)dx}$
Sử dụng máy tính Casio fx 580vnx tính tích phân trên và lưu vào A
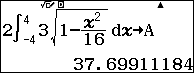
- Tính diện tích mặt phẳng tô màu $latex {{S}_{1}}$
Vì $latex M$ đối xứng với $latex N$ qua $latex Oy$ nên ta có tọa độ điểm $latex M\left( -2\sqrt{3};1.5 \right)$ và phần tô màu bị giới hạn bởi hai đường thẳng $latex x=-2\sqrt{3}$ và $latex x=2\sqrt{3}$
Suy ra: $latex {{S}_{1}}=2\int\limits_{-2\sqrt{3}}^{2\sqrt{3}}{\left( 3\sqrt{1-\dfrac{{{x}^{2}}}{16}} \right)dx}$
Sử dụng máy tính Casio fx 580vnx tính tích phân trên và lưu vào B
Diện tích mặt phẳng tô màu: $latex {{S}_{2}}={{S}_{\left( E \right)}}-{{S}_{1}}=A-B$
Vậy số tiền để sơn bảng quảng cáo là: $latex 200000B+100000(A-B)$
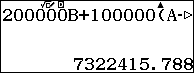
Đáp án A
Cảm ơn các bạn đã theo dõi bài viết SỬ DỤNG MÁY TÍNH CASIO fx 580vnx GIẢI QUYẾT CÁC BÀI TOÁN TÍCH PHÂN HAY TRONG ĐỀ THI THAM KHẢO 2019. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO.
About Ngọc Hiền Bitex
