BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tìm trung vị của mẫu số liệu ghép nhóm
- 20/11/2023
- 307 lượt xem
Giả sử ta có mẫu số liệu ghép nhóm:
Ta tính thêm tần số tích luỹ $\displaystyle c_k=\sum_{i=1}^{k}n_i\ (k=1,2,3,\dots )$, hiệu $\dfrac{c_n}{2}-M_i\ (i=1,2,3\dots, n)$ và có bảng:
Công thức: $\qquad \qquad M_e=a_m+\dfrac{M_{m-1}}{n_m}.(a_{m+1}-a_m)$ trong đó $m$ được chọn sao cho $M_m$ là số âm đầu tiên trong các số $M_i$, $i=1,2,3,\dots n$ |
| $\ \ a_1\ \ $ | $\ \ a_2\ \ $ | $\ \ a_3\ $ | $\ \ a_4 \ \ $ | $\ \ a_5\ \ $ | $\ \ a_6\ \ $ |
| $\ \ 150\ \ $ | $\ \ 155\ \ $ | $\ \ 160\ $ | $\ \ 165 \ \ $ | $\ \ 170\ \ $ | $\ \ 175\ \ $ |
| $\ \ 1\ \ $ | $\ \ 7\ \ $ | $\ \ 12\ \ $ | $\ \ 3\ \ $ | $\ \ 2\ \ $ | |
| $\ \ 1\ \ $ | $\ \ 8\ \ $ | $\ \ 20\ \ $ | $\ \ 23\ \ $ | $\ \ 25\ \ $ | |
| $\ \ 11,5\ \ $ | $\ \ 4,5\ \ $ | $\ \ -7,5\ \ $ | $\ \ -11,5\ \ $ | $\ \ -12,5\ \ $ |
Ta thấy $-7,5$ là số âm đầu tiên nên $a_m=a_3$.
Khi đó: $$M_e=160+\dfrac{4,5}{12}.5=$$
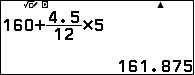
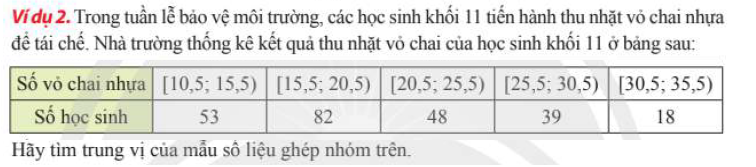
| $\ \ a_1\ \ $ | $\ \ a_2\ \ $ | $\ \ a_3\ $ | $\ \ a_4 \ \ $ | $\ \ a_5\ \ $ | $\ \ a_6\ \ $ |
| $\ \ 10,5\ \ $ | $\ \ 15,5\ \ $ | $\ \ 20,5\ $ | $\ \ 25,5 \ \ $ | $\ \ 30,5\ \ $ | $\ \ 35,5\ \ $ |
| $\ \ 53\ \ $ | $\ \ 82\ \ $ | $\ \ 48 \ $ | $\ \ 39\ \ $ | $\ \ 18\ \ $ | |
| $\ \ 53\ \ $ | $\ \ 135\ \ $ | $\ \ 183\ \ $ | $\ \ 222\ \ $ | $\ \ 240\ \ $ | |
| $\ \ 67\ \ $ | $\ \ -15\ \ $ | $\ \ -63\ \ $ | $\ \ -102\ \ $ | $\ \ -120\ \ $ |
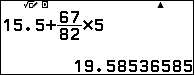
Ta thấy $-15$ là số âm đầu tiên. Vậy $a_m=a_2$. Khi đó:
$$M_e=15,5+\dfrac{67}{82}.5$$
Chia sẻ
About TS. Nguyễn Thái Sơn
