BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
HƯỚNG DẪN GIẢI MINIGAMES LIVESTREAM ÔN TẬP THI THPT QUỐC GIA 2019 MÔN TOÁN - CHUYÊN ĐỀ ĐẠI SỐ NGÀY 09/06/2019
- 17/06/2019
- 435 lượt xem
Dưới đây là lời giải chi tiết cho phần thi minigames livestream ôn tập thi THPT Quốc Gia 2019 môn Toán- chuyên đề đại số ngày 09/06/2019
Có bao nhiêu số nguyên $m$ để phương trình: $x+3=m{{3}^{x}}$ có hai nghiệm phân biệt
A. 7
B. 6
C. 5
D. 9
.[/dropshadowbox]
Hướng dẫn giải
Ta có $x+3=m{{3}^{x}}$ $\Leftrightarrow m=\dfrac{x+3}{{{3}^{x}}}$
Suy ra ycbt tương đương với phương trình $m=\dfrac{x+3}{{{3}^{x}}}$có hai nghiệm phân biệt
Xét hàm số $f\left( x \right)=\dfrac{x+3}{{{3}^{x}}}$
$\Rightarrow {{f}^{/}}\left( x \right)=\dfrac{{{3}^{x}}-{{3}^{x}}\left( x+3 \right)\ln 3}{{{\left( {{3}^{x}} \right)}^{2}}}=\dfrac{1-\left( x+3 \right)\ln 3}{{{3}^{x}}}$
${{f}^{/}}\left( x \right)=0\Leftrightarrow x=\dfrac{1}{\ln 3}-3$
Bảng biến thiên:
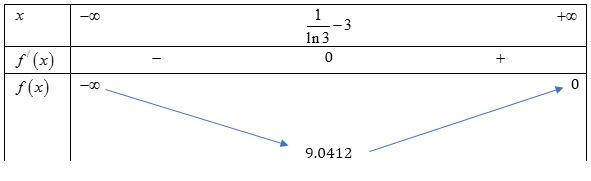
Theo bảng biến thiên ta có phương trình $m=\dfrac{x+3}{{{3}^{x}}}$có hai nghiệm phân biệt khi và chỉ khi $0<m<9.0412$
Vậy có 9 giá trị $m$ thỏa điều kiện bài toán.
Đáp án D
Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
